7.1 Work
Learning Objectives
By the end of this section, you will be able to:
- Represent the work done by any force
- Evaluate the work done for various forces
In physics, work is done on an object when energy is transferred to the object. In other words, work is done when a force acts on something that undergoes a displacement from one position to another. Forces can vary as a function of position, and displacements can be along various paths between two points. We first define the increment of work dW done by a force acting through an infinitesimal displacement as the dot product of these two vectors:
Then, we can add up the contributions for infinitesimal displacements, along a path between two positions, to get the total work.
Work Done by a Force
The work done by a force is the integral of the force with respect to displacement along the path of the displacement:
The vectors involved in the definition of the work done by a force acting on a particle are illustrated in Figure 7.2. While in general, Equation 7.2 requires mathematics beyond the scope of this text, in many simple situations this integral becomes a familiar integral in one variable. We will examine several such examples and restrict our discussion to these cases.
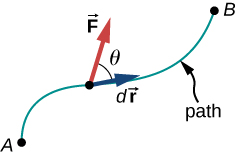
We choose to express the dot product in terms of the magnitudes of the vectors and the cosine of the angle between them, because the meaning of the dot product for work can be put into words more directly in terms of magnitudes and angles. We could equally well have expressed the dot product in terms of the various components introduced in Vectors. In two dimensions, these were the x- and y-components in Cartesian coordinates, or the r- and -components in polar coordinates; in three dimensions, it was just x-, y-, and z-components. Which choice is more convenient depends on the situation. In words, you can express Equation 7.1 for the work done by a force acting over a displacement as a product of one component acting parallel to the other component. From the properties of vectors, it doesn’t matter if you take the component of the force parallel to the displacement or the component of the displacement parallel to the force—you get the same result either way.
Recall that the magnitude of a force times the cosine of the angle the force makes with a given direction is the component of the force in the given direction. The components of a vector can be positive, negative, or zero, depending on whether the angle between the vector and the component-direction is between and or and , or is equal to . As a result, the work done by a force can be positive, negative, or zero, depending on whether the force is generally in the direction of the displacement, generally opposite to the displacement, or perpendicular to the displacement. The maximum work is done by a given force when it is along the direction of the displacement (), and zero work is done when the force is perpendicular to the displacement ().
The units of work are units of force multiplied by units of length, which in the SI system is newtons times meters, This combination is called a joule, for historical reasons that we will mention later, and is abbreviated as J. In the English system, still used in the United States, the unit of force is the pound (lb) and the unit of distance is the foot (ft), so the unit of work is the foot-pound
Work Done by Constant Forces and Contact Forces
The simplest work to evaluate is that done by a force that is constant in magnitude and direction. In this case, we can factor out the force; the remaining integral is just the total displacement, which only depends on the end points A and B, but not on the path between them:
Figure 7.3(a) shows a person exerting a constant force along the handle of a lawn mower, which makes an angle with the horizontal. The horizontal displacement of the lawn mower, over which the force acts, is The work done on the lawn mower is, which the figure also illustrates as the horizontal component of the force times the magnitude of the displacement.
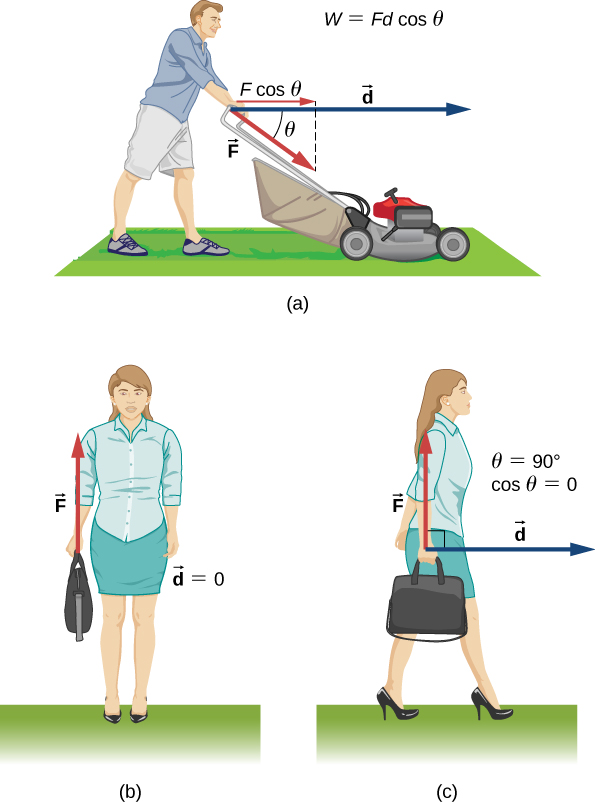
Figure 7.3(b) shows a person holding a briefcase. The person must exert an upward force, equal in magnitude to the weight of the briefcase, but this force does no work, because the displacement over which it acts is zero.
In Figure 7.3(c), where the person in (b) is walking horizontally with constant speed, the work done by the person on the briefcase is still zero, but now because the angle between the force exerted and the displacement is ( perpendicular to ) and .
Example 7.1
Calculating the Work You Do to Push a Lawn Mower
How much work is done on the lawn mower by the person in Figure 7.3(a) if he exerts a constant force of 75.0 N at an angle below the horizontal and pushes the mower 25.0 m on level ground?Strategy
We can solve this problem by substituting the given values into the definition of work done on an object by a constant force, stated in the equation . The force, angle, and displacement are given, so that only the work W is unknown.Solution
The equation for the work isSubstituting the known values gives
Significance
Even though one and a half kilojoules may seem like a lot of work, we will see in Potential Energy and Conservation of Energy that it’s only about as much work as you could do by burning one sixth of a gram of fat.When you mow the grass, other forces act on the lawn mower besides the force you exert—namely, the contact force of the ground and the gravitational force of Earth. Let’s consider the work done by these forces in general. For an object moving on a surface, the displacement is tangent to the surface. The part of the contact force on the object that is perpendicular to the surface is the normal force Since the cosine of the angle between the normal and the tangent to a surface is zero, we have
The normal force never does work under these circumstances. (Note that if the displacement did have a relative component perpendicular to the surface, the object would either leave the surface or break through it, and there would no longer be any normal contact force. However, if the object is more than a particle, and has an internal structure, the normal contact force can do work on it, for example, by displacing it or deforming its shape. This will be mentioned in the next chapter.)
The part of the contact force on the object that is parallel to the surface is friction, For this object sliding along the surface, kinetic friction is opposite to relative to the surface, so the work done by kinetic friction is negative. If the magnitude of is constant (as it would be if all the other forces on the object were constant), then the work done by friction is
where is the path length on the surface. The force of static friction does no work in the reference frame between two surfaces because there is never displacement between the surfaces. As an external force, static friction can do work. Static friction can keep someone from sliding off a sled when the sled is moving and perform positive work on the person. If you’re driving your car at the speed limit on a straight, level stretch of highway, the negative work done by air resistance is balanced by the positive work done by the static friction of the road on the drive wheels. You can pull the rug out from under an object in such a way that it slides backward relative to the rug, but forward relative to the floor. In this case, kinetic friction exerted by the rug on the object could be in the same direction as the displacement of the object, relative to the floor, and do positive work. The bottom line is that you need to analyze each particular case to determine the work done by the forces, whether positive, negative or zero.
Example 7.2
Moving a Couch
You decide to move your couch to a new position on your horizontal living room floor. The normal force on the couch is 1 kN and the coefficient of friction is 0.6. (a) You first push the couch 3 m parallel to a wall and then 1 m perpendicular to the wall (A to B in Figure 7.4). How much work is done by the frictional force? (b) You don’t like the new position, so you move the couch straight back to its original position (B to A in Figure 7.4). What was the total work done against friction moving the couch away from its original position and back again?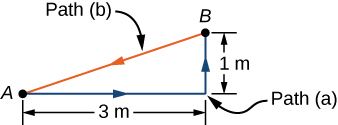
Strategy
The magnitude of the force of kinetic friction on the couch is constant, equal to the coefficient of friction times the normal force, . Therefore, the work done by it is , where d is the path length traversed. The segments of the paths are the sides of a right triangle, so the path lengths are easily calculated. In part (b), you can use the fact that the work done against a force is the negative of the work done by the force.Solution
- The work done by friction i
- The length of the path along the hypotenuse is , so the total work done against friction is
Significance
The total path over which the work of friction was evaluated began and ended at the same point (it was a closed path), so that the total displacement of the couch was zero. However, the total work was not zero. The reason is that forces like friction are classified as nonconservative forces, or dissipative forces, as we discuss in the next chapter.Check Your Understanding 7.1
Can kinetic friction ever be a constant force for all paths?
The other force on the lawn mower mentioned above was Earth’s gravitational force, or the weight of the mower. Near the surface of Earth, the gravitational force on an object of mass m has a constant magnitude, mg, and constant direction, vertically down. Therefore, the work done by gravity on an object is the dot product of its weight and its displacement. In many cases, it is convenient to express the dot product for gravitational work in terms of the x-, y-, and z-components of the vectors. A typical coordinate system has the x-axis horizontal and the y-axis vertically up. Then the gravitational force is so the work done by gravity, over any path from A to B, is
The work done by a constant force of gravity on an object depends only on the object’s weight and the difference in height through which the object is displaced. Gravity does negative work on an object that moves upward (), or, in other words, you must do positive work against gravity to lift an object upward. Alternately, gravity does positive work on an object that moves downward (), or you do negative work against gravity to “lift” an object downward, controlling its descent so it doesn’t drop to the ground. (“Lift” is used as opposed to “drop”.)
Example 7.3
Shelving a Book
You lift an oversized library book, weighing 20 N, 1 m vertically down from a shelf, and carry it 3 m horizontally to a table (Figure 7.5). (a) How much work does gravity do on the book? (b) When you’re finished, you move the book in a straight line back to its original place on the shelf. What was the total work done against gravity, moving the book away from its original position on the shelf and back again?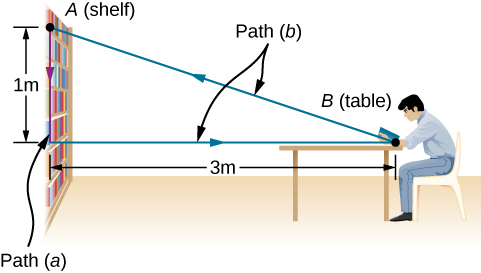
Strategy
We have just seen that the work done by a constant force of gravity depends only on the weight of the object moved and the difference in height for the path taken, . We can evaluate the difference in height to answer (a) and (b).Solution
- Since the book starts on the shelf and is lifted down , we have
- There is zero difference in height for any path that begins and ends at the same place on the shelf, so
Significance
Gravity does positive work (20 J) when the book moves down from the shelf. The gravitational force between two objects is an attractive force, which does positive work when the objects get closer together. Gravity does zero work (0 J) when the book moves horizontally from the shelf to the table and negative work (−20 J) when the book moves from the table back to the shelf. The total work done by gravity is zero Unlike friction or other dissipative forces, described in Example 7.2, the total work done against gravity, over any closed path, is zero. Positive work is done against gravity on the upward parts of a closed path, but an equal amount of negative work is done against gravity on the downward parts. In other words, work done against gravity, lifting an object up, is “given back” when the object comes back down. Forces like gravity (those that do zero work over any closed path) are classified as conservative forces and play an important role in physics.Check Your Understanding 7.2
Can Earth’s gravity ever be a constant force for all paths?
Work Done by Forces that Vary
In general, forces may vary in magnitude and direction at points in space, and paths between two points may be curved. The infinitesimal work done by a variable force can be expressed in terms of the components of the force and the displacement along the path,
Here, the components of the force are functions of position along the path, and the displacements depend on the equations of the path. (Although we chose to illustrate dW in Cartesian coordinates, other coordinates are better suited to some situations.) Equation 7.2 defines the total work as a line integral, or the limit of a sum of infinitesimal amounts of work. The physical concept of work is straightforward: you calculate the work for tiny displacements and add them up. Sometimes the mathematics can seem complicated, but the following example demonstrates how cleanly they can operate.
Example 7.4
Work Done by a Variable Force over a Curved Path
An object moves along a parabolic path from the origin to the point under the action of a force (Figure 7.6). Calculate the work done.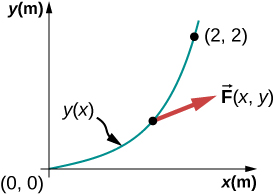
Strategy
The components of the force are given functions of x and y. We can use the equation of the path to express y and dy in terms of x and dx; namely,Then, the integral for the work is just a definite integral of a function of x.
Solution
The infinitesimal element of work isThe integral of is so
Significance
This integral was not hard to do. You can follow the same steps, as in this example, to calculate line integrals representing work for more complicated forces and paths. In this example, everything was given in terms of x- and y-components, which are easiest to use in evaluating the work in this case. In other situations, magnitudes and angles might be easier.Check Your Understanding 7.3
Find the work done by the same force in Example 7.4 over a cubic path, , between the same points and
One very important and widely applicable variable force is the force exerted by a perfectly elastic spring, which satisfies Hooke’s law where k is the spring constant, and is the displacement from the spring’s unstretched (equilibrium) position (Newton’s Laws of Motion). Note that the unstretched position is only the same as the equilibrium position if no other forces are acting (or, if they are, they cancel one another). Forces between molecules, or in any system undergoing small displacements from a stable equilibrium, behave approximately like a spring force.
To calculate the work done by a spring force, we can choose the x-axis along the length of the spring, in the direction of increasing length, as in Figure 7.7, with the origin at the equilibrium position (Then positive x corresponds to a stretch and negative x to a compression.) With this choice of coordinates, the spring force has only an x-component,, and the work done when x changes from to is
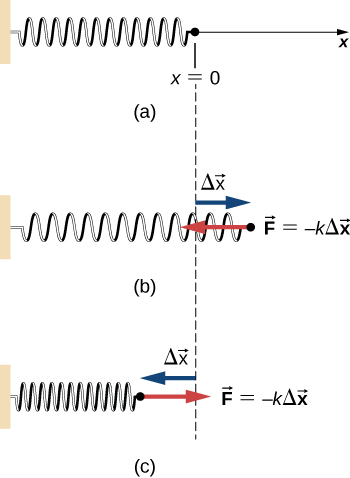
Notice that depends only on the starting and ending points, A and B, and is independent of the actual path between them, as long as it starts at A and ends at B. That is, the actual path could involve going back and forth before ending.
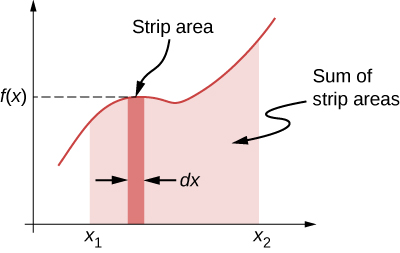
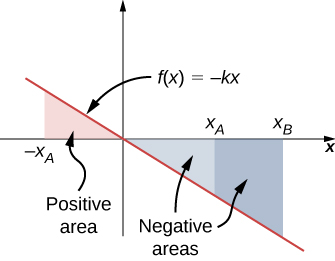
Another interesting thing to notice about Equation 7.5 is that, for this one-dimensional case, you can readily see the correspondence between the work done by a force and the area under the curve of the force versus its displacement. Recall that, in general, a one-dimensional integral is the limit of the sum of infinitesimals,, representing the area of strips, as shown in Figure 7.8. In Equation 7.5, since is a straight line with slope , when plotted versus x, the “area” under the line is just an algebraic combination of triangular “areas,” where “areas” above the x-axis are positive and those below are negative, as shown in Figure 7.9. The magnitude of one of these “areas” is just one-half the triangle’s base, along the x-axis, times the triangle’s height, along the force axis. (There are quotation marks around “area” because this base-height product has the units of work, rather than square meters.)
Example 7.5
Work Done by a Spring Force
A perfectly elastic spring requires 0.54 J of work to stretch 6 cm from its equilibrium position, as in Figure 7.7(b). (a) What is its spring constant k? (b) How much work is required to stretch it an additional 6 cm?Strategy
Work “required” means work done against the spring force, which is the negative of the work in Equation 7.5, that isFor part (a), and ; for part (b), and . In part (a), the work is given and you can solve for the spring constant; in part (b), you can use the value of k, from part (a), to solve for the work.
Solution
- , so
Significance
Since the work done by a spring force is independent of the path, you only needed to calculate the difference in the quantity at the end points. Notice that the work required to stretch the spring from 0 to 12 cm is four times that required to stretch it from 0 to 6 cm, because that work depends on the square of the amount of stretch from equilibrium, . In this circumstance, the work to stretch the spring from 0 to 12 cm is also equal to the work for a composite path from 0 to 6 cm followed by an additional stretch from 6 cm to 12 cm. Therefore, , or , as we found above.Check Your Understanding 7.4
The spring in Example 7.5 is compressed 6 cm from its equilibrium length. (a) Does the spring force do positive or negative work and (b) what is the magnitude?