Position

To describe the motion of an object, you must first be able to describe its position (x): where it is at any particular time. More precisely, we need to specify its position relative to a convenient frame of reference. A frame of reference is an arbitrary set of axes from which the position and motion of an object are described. Earth is often used as a frame of reference, and we often describe the position of an object as it relates to stationary objects on Earth. For example, a rocket launch could be described in terms of the position of the rocket with respect to Earth as a whole, whereas a cyclist’s position could be described in terms of where she is in relation to the buildings she passes Figure 3.2. In other cases, we use reference frames that are not stationary but are in motion relative to Earth. To describe the position of a person in an airplane, for example, we use the airplane, not Earth, as the reference frame. To describe the position of an object undergoing one-dimensional motion, we often use the variable x. Later in the chapter, during the discussion of free fall, we use the variable y.

Figure 3.2 These cyclists in Vietnam can be described by their position relative to buildings or a canal. Their motion can be described by their change in position, or displacement, in a frame of reference. (credit: modification of work by Suzan Black)

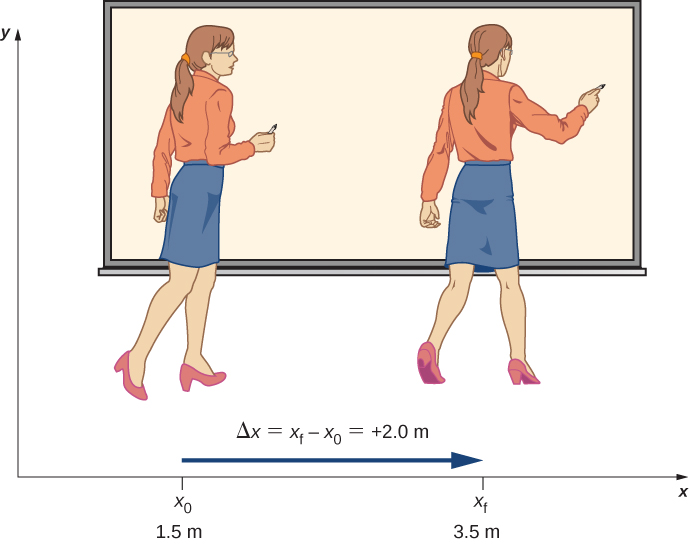
Displacement

If an object moves relative to a frame of reference—for example, if a professor moves to the right relative to a whiteboard Figure 3.3—then the object’s position changes. This change in position is called displacement. The word displacement implies that an object has moved, or has been displaced. Although position is the numerical value of x along a straight line where an object might be located, displacement gives the change in position along this line. Since displacement indicates direction, it is a vector and can be either positive or negative, depending on the choice of positive direction. Also, an analysis of motion can have many displacements embedded in it. If right is positive and an object moves 2 m to the right, then 4 m to the left, the individual displacements are 2 m and $\mathrm{-4}$ m, respectively.

Figure 3.3 A professor paces left and right while lecturing. Her position relative to Earth is given by x. The +2.0-m displacement of the professor relative to Earth is represented by an arrow pointing to the right.

We use the uppercase Greek letter delta (Δ) to mean “change in” whatever quantity follows it; thus, $\text{Δ}x$ means change in position (final position less initial position). We always solve for displacement by subtracting initial position $x_0$ from final position $x_{\text{f}}$. Note that the SI unit for displacement is the meter, but sometimes we use kilometers or other units of length. Keep in mind that when units other than meters are used in a problem, you may need to convert them to meters to complete the calculation (see Appendix B).

Objects in motion can also have a series of displacements. In the previous example of the pacing professor, the individual displacements are 2 m and $\mathrm{-4}$ m, giving a total displacement of −2 m. We define total displacement $\text{Δ}{x}_{\text{Total}}$, as the sum of the individual displacements, and express this mathematically with the equation

where $\text{Δ}{x}_i$ are the individual displacements. In the earlier example,

Similarly,

Thus,

The total displacement is 2 − 4 = −2 m along the x-axis. It is also useful to calculate the magnitude of the displacement, or its size. The magnitude of the displacement is always positive. This is the absolute value of the displacement, because displacement is a vector and cannot have a negative value of magnitude. In our example, the magnitude of the total displacement is 2 m, whereas the magnitudes of the individual displacements are 2 m and 4 m.

The magnitude of the total displacement should not be confused with the distance traveled. Distance traveled $x_{\text{Total}}$, is the total length of the path traveled between two positions. In the previous problem, the distance traveled is the sum of the magnitudes of the individual displacements:

Average Velocity

To calculate the other physical quantities in kinematics we must introduce the time variable. The time variable allows us not only to state where the object is (its position) during its motion, but also how fast it is moving. How fast an object is moving is given by the rate at which the position changes with time.

For each position $x_{\text{i}}$, we assign a particular time $t_{\text{i}}$. If the details of the motion at each instant are not important, the rate is usually expressed as the average velocity $\stackrel{\text{–}}{v}$. This vector quantity is simply the total displacement between two points divided by the time taken to travel between them. The time taken to travel between two points is called the elapsed time $\text{Δ}t$.

It is important to note that the average velocity is a vector and can be negative, depending on positions $x_1$ and $x_2$.

Example 3.1

Delivering Flyers

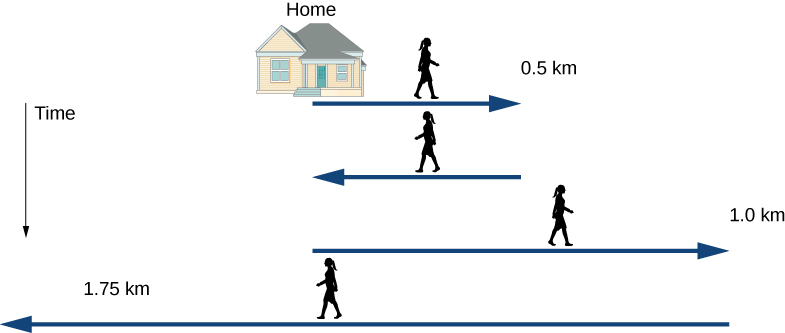
Jill sets out from her home to deliver flyers for her yard sale, traveling due east along her street lined with houses. At $0.5$ km and 9 minutes later she runs out of flyers and has to retrace her steps back to her house to get more. This takes an additional 9 minutes. After picking up more flyers, she sets out again on the same path, continuing where she left off, and ends up 1.0 km from her house. This third leg of her trip takes $15$ minutes. At this point she turns back toward her house, heading west. After $1.75$ km and $25$ minutes she stops to rest.

1. What is Jill’s total displacement to the point where she stops to rest?
2. What is the magnitude of the final displacement?
3. What is the average velocity during her entire trip?
4. What is the total distance traveled?
5. Make a graph of position versus time.

A sketch of Jill’s movements is shown in Figure 3.4.

Figure 3.4 Timeline of Jill’s movements.

Strategy

The problem contains data on the various legs of Jill’s trip, so it would be useful to make a table of the physical quantities. We are given position and time in the wording of the problem so we can calculate the displacements and the elapsed time. We take east to be the positive direction. From this information we can find the total displacement and average velocity. Jill’s home is the starting point $x_0$. The following table gives Jill’s time and position in the first two columns, and the displacements are calculated in the third column.

Time ti (min)	Position $x_i$ (km)	Displacement $\text{Δ}{x}_{\text{i}}$ (km)
$t_0=0$	$x_0=0$	$\text{Δ}{x}_0=0$
$t_1=9$	$x_1=0.5$	$\text{Δ}{x}_1=x_1-x_0=0.5$
$t_2=18$	$x_2=0$	$\text{Δ}{x}_2=x_2-x_1=\mathrm{-0.5}$
$t_3=33$	$x_3=1.0$	$\text{Δ}{x}_3=x_3-x_2=1.0$
$t_4=58$	$x_4=\mathrm{-0.75}$	$\text{Δ}{x}_4=x_4-x_3=\mathrm{-1.75}$

Solution

1. From the above table, the total displacement is
   $${\displaystyle \sum \text{Δ}{x}_{\text{i}}=0.5-0.5+1.0-1.75}\text{km}=\mathrm{-0.75}\text{km}\text{.}$$
2. The magnitude of the total displacement is $\left|\mathrm{-0.75}\right|\text{km}=0.75\text{km}$.
3. $\text{Average velocity}=\frac{\text{Total}\text{displacement}}{\text{Elapsed}\text{time}}=\stackrel{\text{–}}{v}=\frac{\mathrm{-0.75}\text{km}}{58\text{min}}=\mathrm{-0.013}\text{km/min}$
4. The total distance traveled (sum of magnitudes of individual displacements) is $x_{\text{Total}}={\displaystyle \sum \left|\text{Δ}{x}_{\text{i}}\right|=0.5+0.5+1.0+1.75}\text{km}=3.75\text{km}$.
5. We can graph Jill’s position versus time as a useful aid to see the motion; the graph is shown in Figure 3.5.
   

   

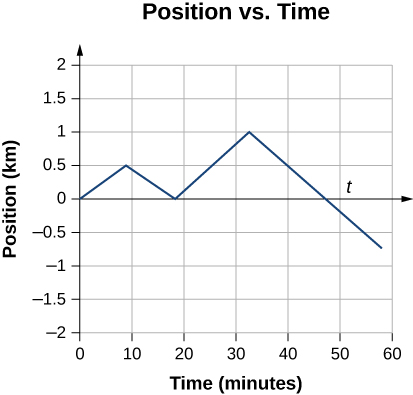   Figure 3.5 This graph depicts Jill’s position versus time. The average velocity is the slope of a line connecting the initial and final points.

Significance

Jill’s total displacement is −0.75 km, which means at the end of her trip she ends up $0.75\text{km}$ due west of her home. The average velocity means if someone was to walk due west at $0.013$ km/min starting at the same time Jill left her home, they both would arrive at the final stopping point at the same time. Note that if Jill were to end her trip at her house, her total displacement would be zero, as well as her average velocity. The total distance traveled during the 58 minutes of elapsed time for her trip is 3.75 km.

Check Your Understanding 3.1

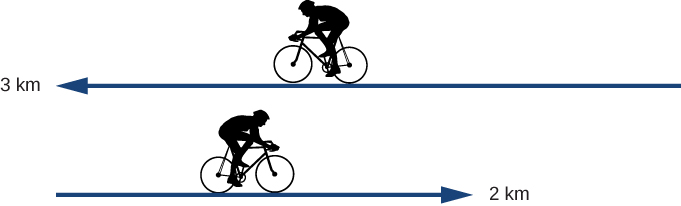
A cyclist rides 3 km west and then turns around and rides 2 km east. (a) What is their displacement? (b) What is the distance traveled? (c) What is the magnitude of their displacement?