Reference Frames

To discuss relative motion in one or more dimensions, we first introduce the concept of reference frames. When we say an object has a certain velocity, we must state it has a velocity with respect to a given reference frame. In most examples we have examined so far, this reference frame has been Earth. If you say a person is sitting in a train moving at 10 m/s east, then you imply the person on the train is moving relative to the surface of Earth at this velocity, and Earth is the reference frame. We can expand our view of the motion of the person on the train and say Earth is spinning in its orbit around the Sun, in which case the motion becomes more complicated. In this case, the solar system is the reference frame. In summary, all discussion of relative motion must define the reference frames involved. We now develop a method to refer to reference frames in relative motion. This method makes an approximation that breaks down near the speed of light, where the more accurate methods or special relativity are needed, but is extremely accurate for everyday speeds (Relativity).

Relative Motion in One Dimension

We introduce relative motion in one dimension first, because the velocity vectors simplify to having only two possible directions. Take the example of the person sitting in a train moving east. If we choose east as the positive direction and Earth as the reference frame, then we can write the velocity of the train with respect to the Earth as ${\overrightarrow{v}}_{\text{TE}}=10\text{m}\text{/}\text{s}\widehat{i}$ east, where the subscripts TE refer to train and Earth. Let’s now say the person gets up out of her seat and walks toward the back of the train at 2 m/s. This tells us she has a velocity relative to the reference frame of the train. Since the person is walking west, in the negative direction, we write her velocity with respect to the train as ${\overrightarrow{v}}_{\text{PT}}=\mathrm{-2}\text{m}\text{/}\text{s}\widehat{i}\text{.}$ We can add the two velocity vectors to find the velocity of the person with respect to Earth. This relative velocity is written as

Note the ordering of the subscripts for the various reference frames in Equation 4.33. The subscripts for the coupling reference frame, which is the train, appear consecutively in the right-hand side of the equation. Figure 4.24 shows the correct order of subscripts when forming the vector equation.

Figure 4.24 When constructing the vector equation, the subscripts for the coupling reference frame appear consecutively on the inside. The subscripts on the left-hand side of the equation are the same as the two outside subscripts on the right-hand side of the equation.

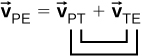
Adding the vectors, we find ${\overrightarrow{v}}_{\text{PE}}=8\text{m}\text{/}\text{s}\widehat{i}\text{,}$ so the person is moving 8 m/s east with respect to Earth. Graphically, this is shown in Figure 4.25.

Figure 4.25 Velocity vectors of the train with respect to Earth, person with respect to the train, and person with respect to Earth.

Relative Velocity in Two Dimensions

We can now apply these concepts to describing motion in two dimensions. Consider a particle P and reference frames S and $S^{\prime },$ as shown in Figure 4.26. The position of the origin of $S^{\prime }$ as measured in S is ${\overrightarrow{r}}_{S^{\prime }S},$ the position of P as measured in $S^{\prime }$ is ${\overrightarrow{r}}_{P{S}^{\prime }},$ and the position of P as measured in S is ${\overrightarrow{r}}_{PS}.$

Figure 4.26 The positions of particle P relative to frames S and $S^{\prime }$ are ${\overrightarrow{r}}_{PS}$ and ${\overrightarrow{r}}_{P{S}^{\prime }},$ respectively.

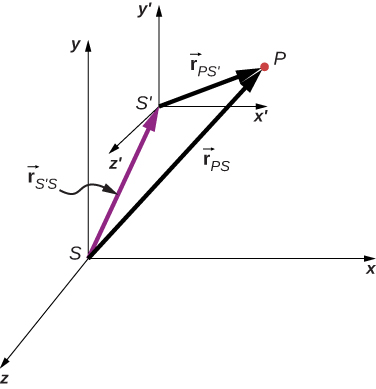
From Figure 4.26 we see that

The relative velocities are the time derivatives of the position vectors. Therefore,

The velocity of a particle relative to S is equal to its velocity relative to $S^{\prime }$ plus the velocity of $S^{\prime }$ relative to S.

We can extend Equation 4.35 to any number of reference frames. For particle P with velocities ${\overrightarrow{v}}_{PA},{\overrightarrow{v}}_{PB}\text{,}\text{and}{\overrightarrow{v}}_{PC}$ in frames A, B, and C,

We can also see how the accelerations are related as observed in two reference frames by differentiating Equation 4.35:

We see that if the velocity of $S^{\prime }$ relative to S is a constant, then ${\overrightarrow{a}}_{S^{\prime }S}=0$ and

This says the acceleration of a particle is the same as measured by two observers moving at a constant velocity relative to each other.

Example 4.13

Motion of a Car Relative to a Truck

A truck is traveling south at a speed of 70 km/h toward an intersection. A car is traveling east toward the intersection at a speed of 80 km/h (Figure 4.27). What is the velocity of the car relative to the truck?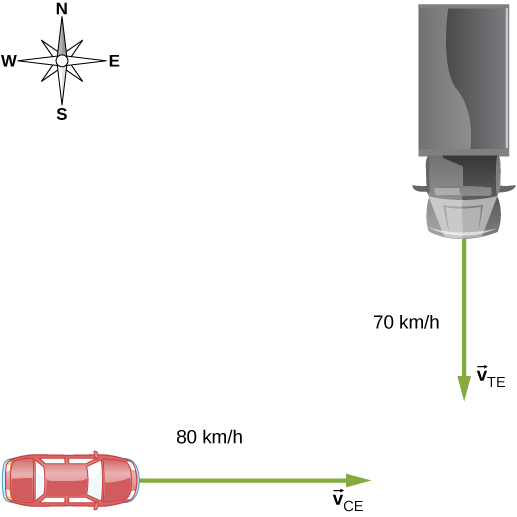

Figure 4.27 A car travels east toward an intersection while a truck travels south toward the same intersection.

Strategy

First, we must establish the reference frame common to both vehicles, which is Earth. Then, we write the velocities of each with respect to the reference frame of Earth, which enables us to form a vector equation that links the car, the truck, and Earth to solve for the velocity of the car with respect to the truck.

Solution

The velocity of the car with respect to Earth is ${\overrightarrow{v}}_{\text{CE}}=80\text{km}\text{/}\text{h}\widehat{i}.$ The velocity of the truck with respect to Earth is ${\overrightarrow{v}}_{\text{TE}}=\mathrm{-70}\text{km}\text{/}\text{h}\widehat{j}\text{.}$ Using the velocity addition rule, the relative motion equation we are seeking is

$${\overrightarrow{v}}_{\text{CT}}={\overrightarrow{v}}_{\text{CE}}+{\overrightarrow{v}}_{\text{ET}}.$$

Here, ${\overrightarrow{v}}_{\text{CT}}$ is the velocity of the car with respect to the truck, and Earth is the connecting reference frame. Since we have the velocity of the truck with respect to Earth, the negative of this vector is the velocity of Earth with respect to the truck: ${\overrightarrow{v}}_{\text{ET}}=\text{−}{\overrightarrow{v}}_{\text{TE}}.$ The vector diagram of this equation is shown in Figure 4.28.

Figure 4.28 Vector diagram of the vector equation ${\overrightarrow{v}}_{\text{CT}}={\overrightarrow{v}}_{\text{CE}}+{\overrightarrow{v}}_{\text{ET}}$.

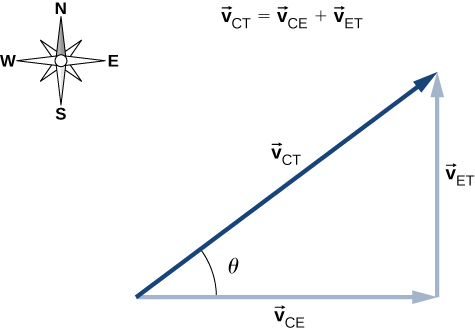
We can now solve for the velocity of the car with respect to the truck:

$$\left|{\overrightarrow{v}}_{\text{CT}}\right|=\sqrt{(80.0\text{km}\text{/}{\text{h})}^2+(70.0\text{km}\text{/}{\text{h})}^2}=106.\text{km}\text{/}\text{h}$$

and

$$\theta ={\text{tan}}^{\mathrm{-1}}\left(\frac{70.0}{80.0}\right)=41.2\text{°}\text{north of east.}$$

Significance

Drawing a vector diagram showing the velocity vectors can help in understanding the relative velocity of the two objects.

Example 4.14

Flying a Plane in a Wind

A pilot must fly a plane due north to reach their destination. The plane can fly at 300 km/h in still air. A wind is blowing out of the northeast at 90 km/h. (a) In what direction must the pilot head the plane to fly due north? (b) What is the speed of the plane relative to the ground?

Strategy

The pilot must point the plane somewhat east of north to compensate for the wind velocity. We need to construct a vector equation that contains the velocity of the plane with respect to the ground, the velocity of the plane with respect to the air, and the velocity of the air with respect to the ground. Since these last two quantities are known, we can solve for the velocity of the plane with respect to the ground. We can graph the vectors and use this diagram to evaluate the magnitude of the plane’s velocity with respect to the ground. The diagram will also tell us the angle the plane’s velocity makes with north with respect to the air, which is the direction the pilot must head the plane.

Solution

The vector equation is ${\overrightarrow{v}}_{\text{PG}}={\overrightarrow{v}}_{\text{PA}}+{\overrightarrow{v}}_{\text{AG}},$ where P = plane, A = air, and G = ground. From the geometry in Figure 4.29, we can solve easily for the magnitude of the velocity of the plane with respect to the ground and the angle of the plane’s heading,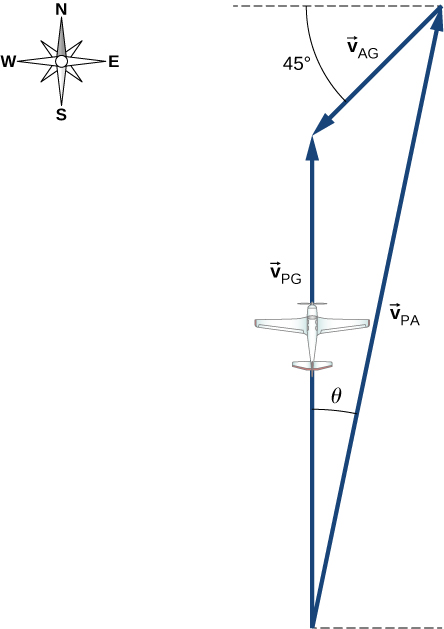 $\theta .$

Figure 4.29 Vector diagram for Equation 4.34 showing the vectors ${\overrightarrow{v}}_{\text{PA}}\text{,}{\overrightarrow{v}}_{\text{AG}},\text{and}{\overrightarrow{v}}_{\text{PG}}.$

Known quantities:

$$\left|{\overrightarrow{v}}_{\text{PA}}\right|=300\text{km}\text{/}\text{h}$$

$$\left|{\overrightarrow{v}}_{\text{AG}}\right|=90\text{km}\text{/}\text{h}$$

(a) In the x direction we have the following:

• $\left|{\overrightarrow{v}}_{\text{PA}}\right|\text{sin}\theta –\left|{\overrightarrow{v}}_{\text{AG}}\right|\text{sin}45\text{°}=0$

• $\theta ={\text{sin}}^{\mathrm{–1}}\left(90\text{km/h}\right)\left(\frac{\text{sin}45\text{°}}{300\text{km/h}}\right)$

• $\theta =12\text{°}$ east of north

(b) In the y direction we have the following:

• $\left|{\overrightarrow{v}}_{\text{PG}}\right|=\left|{\overrightarrow{v}}_{\text{PA}}\right|\text{cos}\theta –\left|{\overrightarrow{v}}_{\text{AG}}\right|\text{cos}45\text{°}$

• $\left|{\overrightarrow{v}}_{\text{PG}}\right|=\left(300\text{km/h}\right)\left(\text{cos}12\text{°}\right)–\left(90\text{km/h}\right)\left(\text{cos}45\text{°}\right)$

• $\left|{\overrightarrow{v}}_{\text{PG}}\right|=230\text{km/h}$