4.2 Acceleration Vector

Learning Objectives

By the end of this section, you will be able to:

Calculate the acceleration vector given the velocity function in unit vector notation.
Describe the motion of a particle with a constant acceleration in three dimensions.
Use the one-dimensional motion equations along perpendicular axes to solve a problem in two or three dimensions with a constant acceleration.
Express the acceleration in unit vector notation.

Instantaneous Acceleration

In addition to obtaining the displacement and velocity vectors of an object in motion, we often want to know its acceleration vector at any point in time along its trajectory. This acceleration vector is the instantaneous acceleration and it can be obtained from the derivative with respect to time of the velocity function, as we have seen in a previous chapter. The only difference in two or three dimensions is that these are now vector quantities. Taking the derivative with respect to time $\vec{v} (t),$ we find

\vec{a} (t) = lim_{∆ t \to 0} \frac{\vec{v} (t + Δ t) - \vec{v} (t)}{Δ t} = \frac{d \vec{v} (t)}{d t} .

4.8

The acceleration in terms of components is

\vec{a} (t) = ​ \frac{d v_{x} (t)}{d t} \hat{i} + \frac{d v_{y} (t)}{d t} \hat{j} + \frac{d v_{z} (t)}{d t} \hat{k} .

4.9

Also, since the velocity is the derivative of the position function, we can write the acceleration in terms of the second derivative of the position function:

\vec{a} (t) = \frac{d^{2} x (t)}{d t^{2}} \hat{i} + \frac{d^{2} y (t)}{d t^{2}} \hat{j} + \frac{d^{2} z (t)}{d t^{2}} \hat{k} .

4.10

Example 4.4

Finding an Acceleration Vector

A particle has a velocity of

\vec{v} (t) = 5.0 t \hat{i} + t^{2} \hat{j} - 2.0 t^{3} \hat{k} m/s .

(a) What is the acceleration function? (b) What is the acceleration vector at t = 2.0 s? Find its magnitude and direction.

Solution

(a) We take the first derivative with respect to time of the velocity function to find the acceleration. The derivative is taken component by component:

\vec{a} (t) = 5.0 \hat{i} + 2.0 t \hat{j} - 6.0 t^{2} \hat{k} m/ s^{2} .

(b) Evaluating $\vec{a} (2.0 s) = 5.0 \hat{i} + 4.0 \hat{j} - 24.0 \hat{k} m/ s^{2}$ gives us the direction in unit vector notation. The magnitude of the acceleration is $| \vec{a} (2.0 s) | = \sqrt{{5.0}^{2} + {4.0}^{2} + {(−24.0)}^{2}} = 24.8 m/ s^{2} .$

Significance

In this example we find that acceleration has a time dependence and is changing throughout the motion. Let’s consider a different velocity function for the particle.

Example 4.5

Finding a Particle Acceleration

A particle has a position function

\vec{r} (t) = (10 t - t^{2}) \hat{i} + 5 t \hat{j} + 5 t ​ \hat{k} m .

(a) What is the velocity? (b) What is the acceleration? (c) Describe the motion from t = 0 s.

Strategy

We can gain some insight into the problem by looking at the position function. It is linear in y and z, so we know the acceleration in these directions is zero when we take the second derivative. Also, note that the position in the x direction is zero for t = 0 s and t = 10 s.

Solution

(a) Taking the derivative with respect to time of the position function, we find

\vec{v} (t) = (10 - 2 t) \hat{i} + 5 \hat{j} + 5 \hat{k} m/s .

The velocity function is linear in time in the x direction and is constant in the y and z directions.

(b) Taking the derivative of the velocity function, we find

\vec{a} (t) = −2 \hat{i} {m/s}^{2} .

The acceleration vector is a constant in the negative x-direction.

(c) The trajectory of the particle can be seen in Figure 4.9. Let’s look in the y and z directions first. The particle’s position increases steadily as a function of time with a constant velocity in these directions. In the x direction, however, the particle follows a path in positive x until t = 5 s, when it reverses direction. We know this from looking at the velocity function, which becomes zero at this time and negative thereafter. We also know this because the acceleration is negative and constant—meaning, the particle is accelerating in the opposite direction. The particle’s position reaches 25 m, where it then reverses direction and begins to accelerate in the negative x direction. The position reaches zero at t = 10 s.

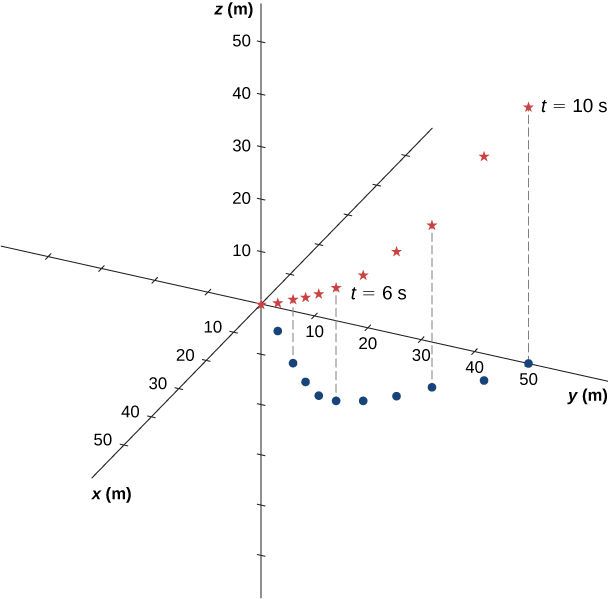
An x y z coordinate system is shown. All the axes show distance in meters and run from -50 to 50 meters. A series of 10 red stars are shown, with the sixth star is labeled as t = 6 s and the tenth as t = 10 s. The red series of stars starts at the origin and curves upward (both y and z increasing with time). Vertical dashed lines connect the red dots to a series of blue dots in the x y plane. The blue dots are all in the first quadrant (positive x and y). The dots are regularly spaced along the y coordinate, while the x coordinate starts at 0, increases, reaches a maximum of x = 25 m at t = 5, and then decreases back to x = 0 at t 10 s.

Figure 4.9 The particle starts at point (x, y, z) = (0, 0, 0) with position vector

\vec{r} = 0

as shown with red stars. The projection of the trajectory onto the xy-plane is shown with blue dots. The values of y and z increase linearly as a function of time, whereas x has a turning point at t = 5 s and 25 m, when it reverses direction. At this point, the x component of the velocity becomes negative. At t = 10 s, the particle is back to 0 m in the x direction.

Significance

By graphing the trajectory of the particle, we can better understand its motion, given by the numerical results of the kinematic equations.

Check Your Understanding 4.2

Suppose the acceleration function has the form $\vec{a} (t) = a \hat{i} + b \hat{j} + c \hat{k} m/ s^{2},$ where a, b, and c are constants. What can be said about the functional form of the velocity function?

Constant Acceleration

Multidimensional motion with constant acceleration can be treated the same way as shown in the previous chapter for one-dimensional motion. Earlier we showed that three-dimensional motion is equivalent to three one-dimensional motions, each along an axis perpendicular to the others. To develop the relevant equations in each direction, let’s consider the two-dimensional problem of a particle moving in the xy plane with constant acceleration, ignoring the z-component for the moment. The acceleration vector is

\vec{a} = a_{0 x} \hat{i} + a_{0 y} \hat{j} .

Each component of the motion has a separate set of equations similar to Equation 3.10–Equation 3.14 of the previous chapter on one-dimensional motion. We show only the equations for position and velocity in the x- and y-directions. A similar set of kinematic equations could be written for motion in the z-direction:

x (t) = x_{0} + {(v_{x})}_{avg} t

4.11

v_{x} (t) = v_{0 x} + a_{x} t

4.12

x (t) = x_{0} + v_{0 x} t + \frac{1}{2} a_{x} t^{2}

4.13

v_{x}^{2} (t) = v_{0 x}^{2} + 2 a_{x} (x - x_{0})

4.14

y (t) = y_{0} + {(v_{y})}_{avg} t

4.15

v_{y} (t) = v_{0 y} + a_{y} t

4.16

y (t) = y_{0} + v_{0 y} t + \frac{1}{2} a_{y} t^{2}

4.17

v_{y}^{2} (t) = v_{0 y}^{2} + 2 a_{y} (y - y_{0}) .

4.18

Here the subscript 0 denotes the initial position or velocity. Equation 4.11 to Equation 4.18 can be substituted into Equation 4.2 and Equation 4.5 without the z-component to obtain the position vector and velocity vector as a function of time in two dimensions:

\vec{r} (t) = x (t) \hat{i} + y (t) \hat{j} and \vec{v} (t) = v_{x} (t) \hat{i} + v_{y} (t) \hat{j} .

The following example illustrates a practical use of the kinematic equations in two dimensions.

Example 4.6

A Skier

Figure 4.10 shows a skier moving with an acceleration of

2.1 m/ s^{2}

down a slope of

15 °

at t = 0. With the origin of the coordinate system at the front of the lodge, her initial position and velocity are

\vec{r} (0) = (75.0 \hat{i} - 50.0 \hat{j}) m

and

\vec{v} (0) = (4.1 \hat{i} - 1.1 \hat{j}) m/s .

(a) What are the x- and y-components of the skier’s position and velocity as functions of time? (b) What are her position and velocity at t = 10.0 s?

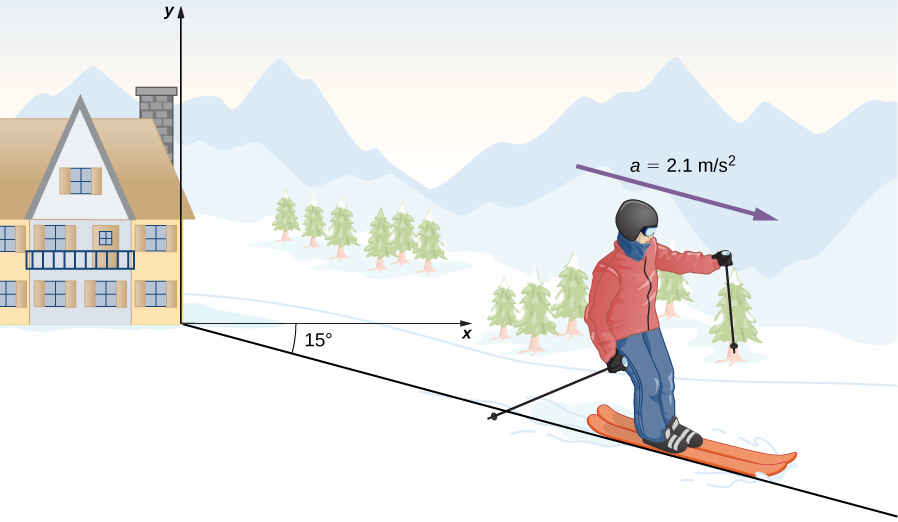
An illustration of a skier in an x y coordinate system is shown. The skier is moving along a line that is 15 degrees below the horizontal x direction and has an acceleration of a = 2.1 meters per second squared also directed in his direction of motion. The acceleration is represented as a purple arrow.

Figure 4.10 A skier has an acceleration of

2.1 {m/s}^{2}

down a slope of

15 ° .

The origin of the coordinate system is at the ski lodge.

Strategy

Since we are evaluating the components of the motion equations in the x and y directions, we need to find the components of the acceleration and put them into the kinematic equations. The components of the acceleration are found by referring to the coordinate system in Figure 4.10. Then, by inserting the components of the initial position and velocity into the motion equations, we can solve for her position and velocity at a later time t.

Solution

(a) The origin of the coordinate system is at the top of the hill with y-axis vertically upward and the x-axis horizontal. By looking at the trajectory of the skier, the x-component of the acceleration is positive and the y-component is negative. Since the angle is

15 °

down the slope, we find

a_{x} = (2.1 m/ s^{2}) cos (15 °) = 2.0 m/ s^{2}

a_{y} = (−2.1 m/ s^{2}) sin 15 ° = −0.54 m/ s^{2} .

Inserting the initial position and velocity into Equation 4.12 and Equation 4.13 for x, we have

x (t) = 75.0 m + (4.1 m/s) t + \frac{1}{2} (2.0 m/ s^{2}) t^{2}

v_{x} (t) = 4.1 m/s + (2.0 m/ s^{2}) t .

For y, we have

y (t) = −50.0 m + (−1.1 m/s) t + \frac{1}{2} (−0.54 m/ s^{2}) t^{2}

v_{y} (t) = −1.1 m/s + (−0.54 m/ s^{2}) t .

(b) Now that we have the equations of motion for x and y as functions of time, we can evaluate them at t = 10.0 s:

x (10.0 s) = 75.0 m + (4.1 m/ s^{2}) (10.0 s) + \frac{1}{2} (2.0 m/ s^{2}) {(10.0 s)}^{2} = 216.0 m

v_{x} (10.0 s) = 4.1 m/s + (2.0 m/ s^{2}) (10.0 s) = 24.1 m /s

y (10.0 s) = −50.0 m + (−1.1 m/s) (10.0 s) + \frac{1}{2} (−0.54 m/ s^{2}) {(10.0 s)}^{2} = −88.0 m

v_{y} (10.0 s) = −1.1 m/s + (−0.54 m/ s^{2}) (10.0 s) = −6.5 m/s .

The position and velocity at t = 10.0 s are, finally,

\vec{r} (10.0 s) = (216.0 \hat{i} - 88.0 \hat{j}) m

\vec{v} (10.0 s) = (24.1 \hat{i} - 6.5 \hat{j}) m/s .

The magnitude of the velocity of the skier at 10.0 s is 25 m/s, which is 60 mi/h.

Significance

It is useful to know that, given the initial conditions of position, velocity, and acceleration of an object, we can find the position, velocity, and acceleration at any later time.

With Equation 4.8 through Equation 4.10 we have completed the set of expressions for the position, velocity, and acceleration of an object moving in two or three dimensions. If the trajectories of the objects look something like the “Red Arrows” in the opening picture for the chapter, then the expressions for the position, velocity, and acceleration can be quite complicated. In the sections to follow we examine two special cases of motion in two and three dimensions by looking at projectile motion and circular motion.

Interactive

At this University of Colorado Boulder website, you can explore the position velocity and acceleration of a ladybug with an interactive simulation that allows you to change these parameters.