Challenge Problems
World’s Longest Par 3. The tee of the world’s longest par 3 sits atop South Africa’s Hanglip Mountain at 400.0 m above the green and can only be reached by helicopter. The horizontal distance to the green is 359.0 m. Neglect air resistance and answer the following questions. (a) If a golfer launches a shot that is with respect to the horizontal, what initial velocity must she give the ball? (b) What is the time to reach the green?
Use this code chuch to check your answer. This code snippet uses a method called Euler's method to simulate the problem and predict the trajectory of the projectile. Note that the code won't work until you enter in your answer for the initial speed.
Notice that the equations that Euler's method uses to update the position and velocity for each small change in time are simple versions of our kinematic equations. To update the velocity it uses a constant acceleration equation, and to update the position, it uses a constant velocity equation. Even though the acceleration and velocity may not be constant, assuming this is true for a small time interval is often a good approximation, and Euler's method uses this assumption for many small time intervals added together to simulate what the projectile will do.
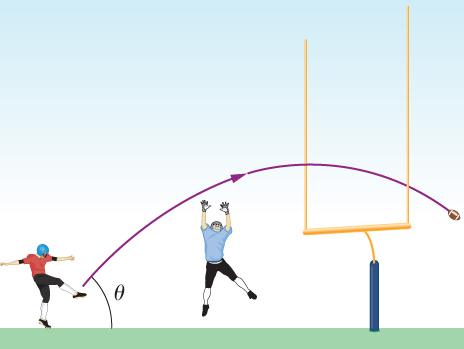
When a field goal kicker kicks a football as hard as he can at to the horizontal, the ball just clears the 3-m-high crossbar of the goalposts 45.7 m away. (a) What is the maximum speed the kicker can impart to the football? (b) In addition to clearing the crossbar, the football must be high enough in the air early during its flight to clear the reach of the onrushing defensive lineman. If the lineman is 4.6 m away and has a vertical reach of 2.5 m, can he block the 45.7-m field goal attempt? (c) What if the lineman is 1.0 m away?
A truck is traveling east at 80 km/h. At an intersection 32 km ahead, a car is traveling north at 50 km/h. (a) How long after this moment will the vehicles be closest to each other? (b) How far apart will they be at that point?