10.6 Torque

Learning Objectives

By the end of this section, you will be able to:

Describe how the magnitude of a torque depends on the magnitude of the lever arm and the angle the force vector makes with the lever arm
Determine the sign (positive or negative) of a torque using the right-hand rule
Calculate individual torques about a common axis and sum them to find the net torque

An important quantity for describing the dynamics of a rotating rigid body is torque. We see the application of torque in many ways in our world. We all have an intuition about torque, as when we use a large wrench to unscrew a stubborn bolt. Torque is at work in unseen ways, as when we press on the accelerator in a car, causing the engine to put additional torque on the drive train. Or every time we move our bodies from a standing position, we apply a torque to our limbs. In this section, we define torque and make an argument for the equation for calculating torque for a rigid body with fixed-axis rotation.

Defining Torque

So far we have defined many variables that are rotational equivalents to their translational counterparts. Let’s consider what the counterpart to force must be. Since forces change the translational motion of objects, the rotational counterpart must be related to changing the rotational motion of an object about an axis. We call this rotational counterpart torque.

In everyday life, we rotate objects about an axis all the time, so intuitively we already know much about torque. Consider, for example, how we rotate a door to open it. First, we know that a door opens slowly if we push too close to its hinges; it is more efficient to rotate a door open if we push far from the hinges. Second, we know that we should push perpendicular to the plane of the door; if we push parallel to the plane of the door, we are not able to rotate it. Third, the larger the force, the more effective it is in opening the door; the harder you push, the more rapidly the door opens. The first point implies that the farther the force is applied from the axis of rotation, the greater the angular acceleration; the second implies that the effectiveness depends on the angle at which the force is applied; the third implies that the magnitude of the force must also be part of the equation. Note that for rotation in a plane, torque has two possible directions. Torque is either clockwise or counterclockwise relative to the chosen pivot point. Figure 10.31 shows counterclockwise rotations.

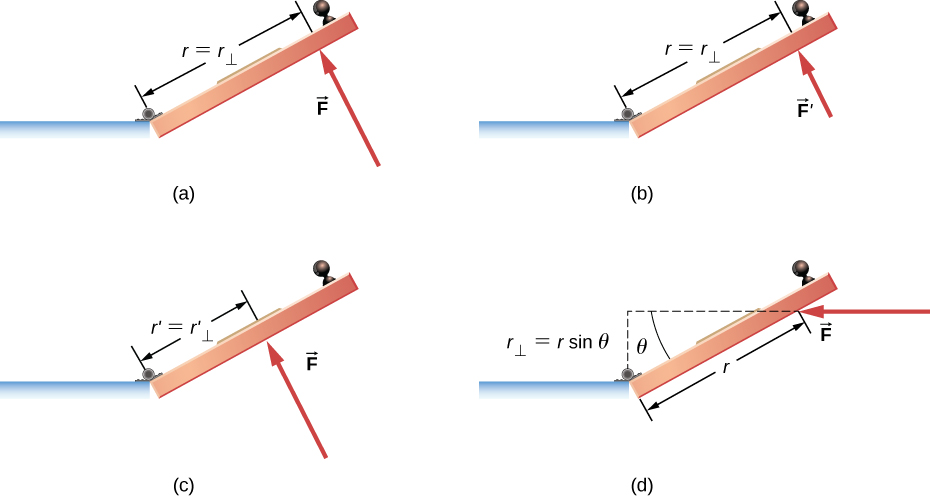
Figure A is a schematic drawing of a door with force F is applied at a distance r from the hinges at a 90 degree angle. Figure B is a schematic drawing of a door with force smaller F is applied at a distance r from the hinges at a 90 degree angle. Figure C is a schematic drawing of a door with force smaller F is applied at a smaller distance r from the hinges at a 90 degree angle. Figure D is a schematic drawing of a door with force F is applied at a distance r from the hinges under the angle theta that is less than 90 degrees.

Figure 10.31 Torque is the turning or twisting effectiveness of a force, illustrated here for door rotation on its hinges (as viewed from overhead). Torque has both magnitude and direction. (a) A counterclockwise torque is produced by a force

\vec{F}

acting at a distance r from the hinges (the pivot point). (b) A smaller counterclockwise torque is produced when a smaller force

{\vec{F}}^{′}

acts at the same distance r from the hinges. (c) The same force as in (a) produces a smaller counterclockwise torque when applied at a smaller distance from the hinges. (d) A smaller counterclockwise torque is produced by the same magnitude force as (a) acting at the same distance as (a) but at an angle

θ

that is less than

90 °

Now let’s consider how to define torques in the general three-dimensional case.

Torque

When a force $\vec{F}$ is applied to a point P whose position is $\vec{r}$ relative to O (Figure 10.32), the torque $\vec{τ}$ around O is

\vec{τ} = \vec{r} \times \vec{F} .

10.22

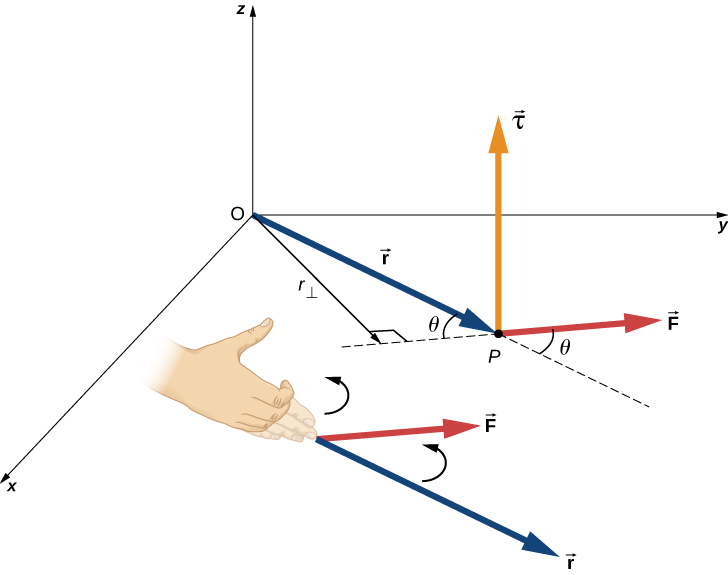
Figure shows an XYZ coordinate system. Force F is applied in the XY plane and is parallel to the X axis. Vector r lies in the XY plane. It starts at the origin of the origin of the coordinate system and ends at the beginning of vector F. Vector for torque starts at the intersection point of r and v vectors. It is perpendicular to the XY plane and is pointed into the Z direction.

Figure 10.32 The torque is perpendicular to the plane defined by

\vec{r} and \vec{F}

and its direction is determined by the right-hand rule.

From the definition of the cross product, the torque $\vec{τ}$ is perpendicular to the plane containing $\vec{r} and \vec{F}$ and has magnitude

| \vec{τ} | = | \vec{r} \times \vec{F} | = r F sin θ,

where $θ$ is the angle between the vectors $\vec{r}$ and $\vec{F}$ . The SI unit of torque is newtons times meters, usually written as $N \cdot m$ . The quantity $r_{⊥} = r sin θ$ is the perpendicular distance from O to the line determined by the vector $\vec{F}$ and is called the lever arm. Note that the greater the lever arm, the greater the magnitude of the torque. In terms of the lever arm, the magnitude of the torque is

| \vec{τ} | = r_{⊥} F .

10.23

The cross product $\vec{r} \times \vec{F}$ also tells us the sign of the torque. In Figure 10.32, the cross product $\vec{r} \times \vec{F}$ is along the positive z-axis, which by convention is a positive torque. If $\vec{r} \times \vec{F}$ is along the negative z-axis, this produces a negative torque.

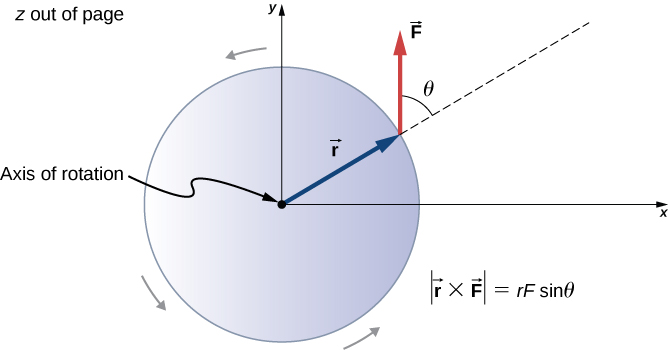
If we consider a disk that is free to rotate about an axis through the center, as shown in Figure 10.33, we can see how the angle between the radius $\vec{r}$ and the force $\vec{F}$ affects the magnitude of the torque. If the angle is zero, the torque is zero; if the angle is $90 °$ , the torque is maximum. The torque in Figure 10.33 is positive because the direction of the torque by the right-hand rule is out of the page along the positive z-axis. The disk rotates counterclockwise due to the torque, in the same direction as a positive angular acceleration.

Figure shows a disk that rotates counterclockwise about its axis through the center.

Figure 10.33 A disk is free to rotate about its axis through the center. The magnitude of the torque on the disk is

r F sin θ

.When

θ = 0 °

, the torque is zero and the disk does not rotate. When

θ = 90 °

, the torque is maximum and the disk rotates with maximum angular acceleration.

Any number of torques can be calculated about a given axis. The individual torques add to produce a net torque about the axis. When the appropriate sign (positive or negative) is assigned to the magnitudes of individual torques about a specified axis, the net torque about the axis is the sum of the individual torques:

{\vec{τ}}_{net} = \sum_{i} {\vec{τ}}_{i} .

10.24

Calculating Net Torque for Rigid Bodies on a Fixed Axis

In the following examples, we calculate the torque both abstractly and as applied to a rigid body.

We first introduce a problem-solving strategy.

Problem-Solving Strategy

Finding Net Torque

Choose a coordinate system with the pivot point or axis of rotation as the origin of the selected coordinate system.
Determine the angle between the lever arm $\vec{r}$ and the force vector.
Take the cross product of $\vec{r} and \vec{F}$ to determine if the torque is positive or negative about the pivot point or axis.
Evaluate the magnitude of the torque using $r_{⊥} F$ .
Assign the appropriate sign, positive or negative, to the magnitude.
Sum the torques to find the net torque.

Example 10.14

Calculating Torque

Four forces are shown in Figure 10.34 at particular locations and orientations with respect to a given xy-coordinate system. Find the torque due to each force about the origin, then use your results to find the net torque about the origin.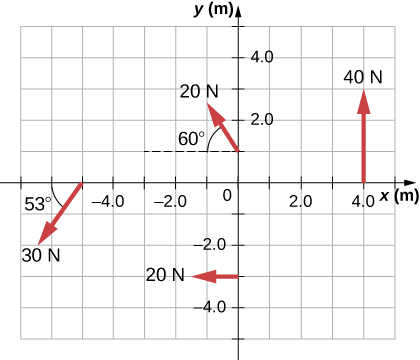

Figure shows four forces producing torques that plotted at the XY coordinate system. Both X and Y axes plot distance in meters. Vector for the force that has a magnitude of 40 N starts at (4,0) point, is parallel to the Y axis, and is directed to the positive direction. Vector for the force that has a magnitude of 20 N starts at (0,-3) point, is parallel to the X axis, and is directed to the negative direction. Another vector for the force that has a magnitude of 20 N starts at (0,1) point, and is directed to the left top part of the graph forming a 60 degree angle with the X axis. Vector for the force that has a magnitude of 30 N starts at (-5,0) point, and is directed to the left bottom part of the graph forming a 53 degree angle with the X axis.

Figure 10.34 Four forces producing torques.

Strategy

This problem requires calculating torque. All known quantities––forces with directions and lever arms––are given in the figure. The goal is to find each individual torque and the net torque by summing the individual torques. Be careful to assign the correct sign to each torque by using the cross product of

\vec{r}

and the force vector

\vec{F}

Solution

Use

| \vec{τ} | = r_{⊥} F = r F sin θ

to find the magnitude and

\vec{τ} = \vec{r} \times \vec{F}

to determine the sign of the torque.

The torque from force 40 N in the first quadrant is given by $(4) (40) sin 90 ° = 160 N \cdot m$ .

The cross product of $\vec{r}$ and $\vec{F}$ is out of the page, positive.

The torque from force 20 N in the third quadrant is given by $− (3) (20) sin 90 ° = - 60 N \cdot m$ .

The cross product of $\vec{r}$ and $\vec{F}$ is into the page, so it is negative.

The torque from force 30 N in the third quadrant is given by $(5) (30) sin 53 ° = 120 N \cdot m$ .

The cross product of $\vec{r}$ and $\vec{F}$ is out of the page, positive.

The torque from force 20 N in the second quadrant is given by $(1) (20) sin 30 ° = 10 N \cdot m$ .

The cross product of $\vec{r}$ and $\vec{F}$ is out of the page.

The net torque is therefore $τ_{net} = \sum_{i} | τ_{i} | = 160 - 60 + 120 + 10 = 230 N \cdot m .$

Significance

Note that each force that acts in the counterclockwise direction has a positive torque, whereas each force that acts in the clockwise direction has a negative torque. The torque is greater when the distance, force, or perpendicular components are greater.

Example 10.15

Calculating Torque on a rigid body

Figure 10.35 shows several forces acting at different locations and angles on a flywheel. We have

| {\vec{F}}_{1} | = 20 N,

| {\vec{F}}_{2} | = 30 N

| {\vec{F}}_{3} | = 30 N

, and

r = 0.5 m

. Find the net torque on the flywheel about an axis through the center.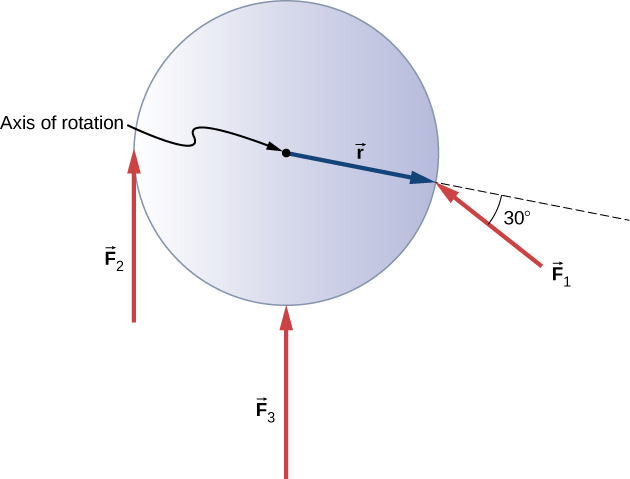

Figure shows a flywheel with three forces acting on it at different locations and angles. Force F3 is applied at the center and is perpendicular to the axis of rotation. Force F2 is applied at the left edge and is perpendicular to the axis of rotation. Force F1 is applied at the center and forms 30 degree angle with the axis of rotation.

Figure 10.35 Three forces acting on a flywheel.

Strategy

We calculate each torque individually, using the cross product, and determine the sign of the torque. Then we sum the torques to find the net torque.

Solution

We start with

{\vec{F}}_{1}

. If we look at Figure 10.35, we see that

{\vec{F}}_{1}

makes an angle of

90 ° + 60 °

with the radius vector

\vec{r}

. Taking the cross product, we see that it is out of the page and so is positive. We also see this from calculating its magnitude:

| {\vec{τ}}_{1} | = r F_{1} sin 150 ° = 0.5 m (20 N) (0.5) = 5.0 N \cdot m .

Next we look at ${\vec{F}}_{2}$ . The angle between ${\vec{F}}_{2}$ and $\vec{r}$ is $90 °$ and the cross product is into the page so the torque is negative. Its value is

| {\vec{τ}}_{2} | = − r F_{2} sin 90 ° = −0.5 m (30 N) = −15.0 N \cdot m .

When we evaluate the torque due to ${\vec{F}}_{3}$ , we see that the angle it makes with $\vec{r}$ is zero so $\vec{r} \times {\vec{F}}_{3} = 0 .$ Therefore, ${\vec{F}}_{3}$ does not produce any torque on the flywheel.

We evaluate the sum of the torques:

τ_{net} = \sum_{i} | τ_{i} | = 5 - 15 = −10 N \cdot m .

Significance

The axis of rotation is at the center of mass of the flywheel. Since the flywheel is on a fixed axis, it is not free to translate. If it were on a frictionless surface and not fixed in place,

{\vec{F}}_{3}

would cause the flywheel to translate, as well as

{\vec{F}}_{1}

. Its motion would be a combination of translation and rotation.

Check Your Understanding 10.6

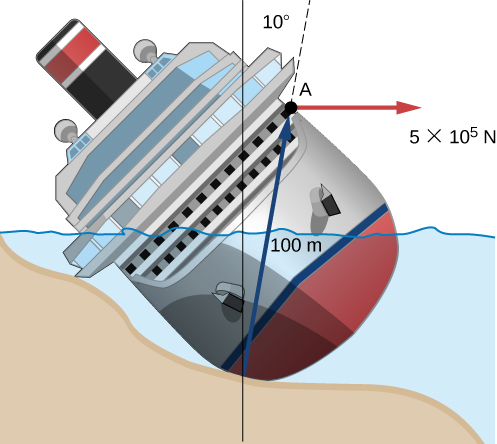
A large ocean-going ship runs aground near the coastline, similar to the fate of the Costa Concordia, and lies at an angle as shown below. Salvage crews must apply a torque to right the ship in order to float the vessel for transport. A force of $5.0 \times 10^{5} N$ acting at point A must be applied to right the ship. What is the torque about the point of contact of the ship with the ground (Figure 10.36)?

Figure shows a ship that lies at an angle on the seashore. A force of 50000 N is applied at 10 degree angle to the normal at a point that 100 meters above the point of contact between the ship and the seashore.

Figure 10.36 A ship runs aground and tilts, requiring torque to be applied to return the vessel to an upright position.