Challenge Problems

144.

A copper wire has a radius of $200 μm$ and a length of 5.0 m. The wire is placed under a tension of 3000 N and the wire stretches by a small amount. The wire is plucked and a pulse travels down the wire. What is the propagation speed of the pulse? (Assume the temperature does not change: $(ρ = 8.96 \frac{g}{{cm}^{3}}, Y = 1.1 \times 10^{11} \frac{N}{m}) .)$

145.

A pulse moving along the x axis can be modeled as the wave function $y (x, t) = 4.00 m e^{− {(\frac{x + (2.00 m/s) t}{1.00 m})}^{2}} .$ (a)What are the direction and propagation speed of the pulse? (b) How far has the wave moved in 3.00 s? (c) Plot the pulse using a spreadsheet at time $t = 0.00 s$ and $t = 3.00 s$ to verify your answer in part (b).

146.

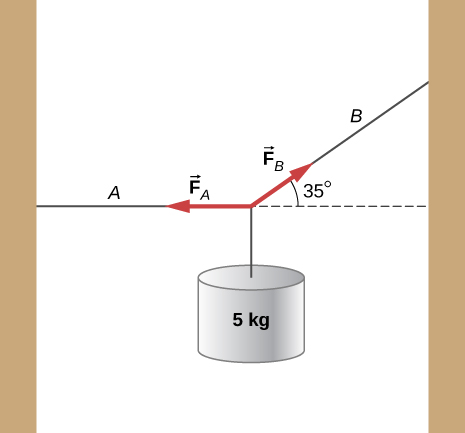
A string with a linear mass density of $μ = 0.0085 kg/m$ is fixed at both ends. A 5.0-kg mass is hung from the string, as shown below. If a pulse is sent along section A, what is the wave speed in section A and the wave speed in section B?

A string is supported at both ends. The left support is lower than the right support. A mass of 5 kg is suspended from its center. The section of string from the left support to the center is horizontal and is labeled A. The section of string from the right support to the centre is labeled B. It makes an angle of 35 degrees with the horizontal. Arrows labeled F subscript A and F subscript B originate from the center of the string and point along the string towards the left support and the right support respectively.

147.

Consider two wave functions $y_{1} (x, t) = A sin (k x - ω t)$ and $y_{2} (x, t) = A sin (k x + ω t + ϕ)$ . What is the wave function resulting from the interference of the two wave? (Hint: $sin (α \pm β) = sin α cos β \pm cos α sin β$ and $ϕ = \frac{ϕ}{2} + \frac{ϕ}{2}$ .)

148.

The wave function that models a standing wave is given as $y_{R} (x, t) = 6.00 cm sin (3.00 m^{−1} x + 1.20 rad)$ $cos (6.00 s^{−1} t + 1.20 rad)$ . What are two wave functions that interfere to form this wave function? Plot the two wave functions and the sum of the sum of the two wave functions at $t = 1.00 s$ to verify your answer.

149.

Consider two wave functions $y_{1} (x, t) = A sin (k x - ω t)$ and $y_{2} (x, t) = A sin (k x + ω t + ϕ)$ . The resultant wave form when you add the two functions is $y_{R} = 2 A sin (k x + \frac{ϕ}{2}) cos (ω t + \frac{ϕ}{2}) .$ Consider the case where $A = 0.03 m^{−1},$ $k = 1.26 m^{−1},$ $ω = π s^{−1}$ , and $ϕ = \frac{π}{10}$ . (a) Where are the first three nodes of the standing wave function starting at zero and moving in the positive x direction? (b) Using a spreadsheet, plot the two wave functions and the resulting function at time $t = 1.00 s$ to verify your answer.