Challenge Problems

89.

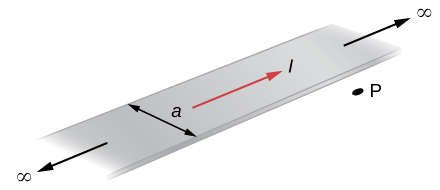
The accompanying figure shows a flat, infinitely long sheet of width a that carries a current I uniformly distributed across it. Find the magnetic field at the point P, which is in the plane of the sheet and at a distance x from one edge. Test your result for the limit $a \to 0 .$

This picture shows a flat, infinitely long sheet of width a that carries a current I uniformly distributed across it. Point P is in the plane of the sheet and at a distance x from one edge.

90.

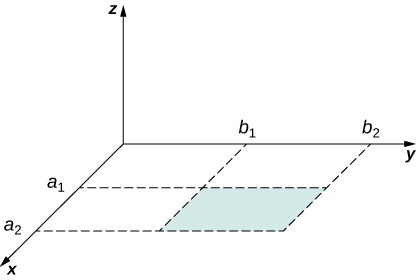
A hypothetical current flowing in the z-direction creates the field $\vec{B} = C [(x / y^{2}) \hat{i} + (1 / y) \hat{j}]$ in the rectangular region of the xy-plane shown in the accompanying figure. Use Ampère’s law to find the current through the rectangle.

This figure shows the rectangular region of the xy-plane; z axis is perpendicular to the plane. Points a1 and a2 are located at the x axis. Points b1 and b2 are located at the y axis. There is an equal distance between all points.

91.

A nonconducting hard rubber circular disk of radius R is painted with a uniform surface charge density $σ .$ It is rotated about its axis with angular speed $ω .$ (a) Find the magnetic field produced at a point on the axis a distance h meters from the center of the disk. (b) Find the numerical value of magnitude of the magnetic field when $σ = 1 {C/m}^{2},$ $R = 20 cm, h = 2 cm,$ and $ω = 400 rad/sec,$ and compare it with the magnitude of magnetic field of Earth, which is about 1/2 Gauss.