7.2 The Heisenberg Uncertainty Principle

Learning Objectives

By the end of this section, you will be able to:

Describe the physical meaning of the position-momentum uncertainty relation
Explain the origins of the uncertainty principle in quantum theory
Describe the physical meaning of the energy-time uncertainty relation

Heisenberg’s uncertainty principle is a key principle in quantum mechanics. Very roughly, it states that if we know everything about where a particle is located (the uncertainty of position is small), we know nothing about its momentum (the uncertainty of momentum is large), and vice versa. Versions of the uncertainty principle also exist for other quantities as well, such as energy and time. We discuss the momentum-position and energy-time uncertainty principles separately.

Momentum and Position

To illustrate the momentum-position uncertainty principle, consider a free particle that moves along the x-direction. The particle moves with a constant velocity u and momentum $p = m u$ . According to de Broglie’s relations, $p = ℏ k$ and $E = ℏ ω$ . As discussed in the previous section, the wave function for this particle is given by

ψ_{k} (x, t) = A [cos (ω t - k x) - i sin (ω t - k x)] = A e^{− i (ω t - k x)} = A e^{− i ω t} e^{i k x}

7.14

and the probability density $| ψ_{k} (x, t) |^{2} = A^{2}$ is uniform and independent of time. The particle is equally likely to be found anywhere along the x-axis but has definite values of wavelength and wave number, and therefore momentum. The uncertainty of position is infinite (we are completely uncertain about position) and the uncertainty of the momentum is zero (we are completely certain about momentum). This account of a free particle is consistent with Heisenberg’s uncertainty principle.

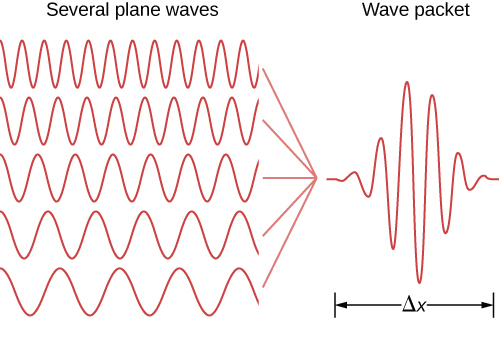
Similar statements can be made of localized particles. In quantum theory, a localized particle is modeled by a linear superposition of free-particle (or plane-wave) states called a wave packet. An example of a wave packet is shown in Figure 7.9. A wave packet contains many wavelengths and therefore by de Broglie’s relations many momenta—possible in quantum mechanics! This particle also has many values of position, although the particle is confined mostly to the interval $Δ x$ . The particle can be better localized $(Δ x$ can be decreased) if more plane-wave states of different wavelengths or momenta are added together in the right way $(Δ p$ is increased). According to Heisenberg, these uncertainties obey the following relation.

The Heisenberg Uncertainty Principle

The product of the uncertainty in position of a particle and the uncertainty in its momentum can never be less than one-half of the reduced Planck constant:

Δ x Δ p \geq ℏ / 2 .

7.15

This relation expresses Heisenberg’s uncertainty principle. It places limits on what we can know about a particle from simultaneous measurements of position and momentum. If $Δ x$ is large, $Δ p$ is small, and vice versa. Equation 7.15 can be derived in a more advanced course in modern physics. Reflecting on this relation in his work The Physical Principles of the Quantum Theory, Heisenberg wrote “Any use of the words ‘position’ and ‘velocity’ with accuracy exceeding that given by [the relation] is just as meaningless as the use of words whose sense is not defined.”

Several waves are shown, all with equal amplitude but different. The result of adding these to form a wave packet is also shown. The wave packet is an oscillating wave whose amplitude increases to a maximum then decreases, so that its envelope is a pulse of width Delta x.

Figure 7.9 Adding together several plane waves of different wavelengths can produce a wave that is relatively localized.

Note that the uncertainty principle has nothing to do with the precision of an experimental apparatus. Even for perfect measuring devices, these uncertainties would remain because they originate in the wave-like nature of matter. The precise value of the product $Δ x Δ p$ depends on the specific form of the wave function. Interestingly, the Gaussian function (or bell-curve distribution) gives the minimum value of the uncertainty product: $Δ x Δ p = ℏ / 2 .$

Example 7.5

The Uncertainty Principle Large and Small

Determine the minimum uncertainties in the positions of the following objects if their speeds are known with a precision of

1.0 \times 10^{−3} m/s

: (a) an electron and (b) a bowling ball of mass 6.0 kg.

Strategy

Given the uncertainty in speed

Δ u = 1.0 \times 10^{−3} m/s

, we have to first determine the uncertainty in momentum

Δ p = m Δ u

and then invert Equation 7.15 to find the uncertainty in position

Δ x = ℏ / (2 Δ p)

Solution

For the electron:
$\begin{matrix} Δ p & = & m Δ u = (9.1 \times 10^{−31} kg) (1.0 \times 10^{−3} m/s) = 9.1 \times 10^{−34} kg \cdot m/s, \\ Δ x & = & \frac{ℏ}{2 Δ p} = 5.8 cm . \end{matrix}$
For the bowling ball:
$\begin{matrix} Δ p & = & m Δ u = (6.0 kg) (1.0 \times 10^{−3} m/s) = 6.0 \times 10^{−3} kg \cdot m/s, \\ Δ x & = & \frac{ℏ}{2 Δ p} = 8.8 \times 10^{−33} m . \end{matrix}$

Significance

Unlike the position uncertainty for the electron, the position uncertainty for the bowling ball is immeasurably small. Planck’s constant is very small, so the limitations imposed by the uncertainty principle are not noticeable in macroscopic systems such as a bowling ball.

Example 7.6

Uncertainty and the Hydrogen Atom

Estimate the ground-state energy of a hydrogen atom using Heisenberg’s uncertainty principle. (Hint: According to early experiments, the size of a hydrogen atom is approximately 0.1 nm.)

Strategy

An electron bound to a hydrogen atom can be modeled by a particle bound to a one-dimensional box of length

L = 0.1 nm .

The ground-state wave function of this system is a half wave, like that given in Example 7.1. This is the largest wavelength that can “fit” in the box, so the wave function corresponds to the lowest energy state. Note that this function is very similar in shape to a Gaussian (bell curve) function. We can take the average energy of a particle described by this function (E) as a good estimate of the ground state energy

(E_{0})

. This average energy of a particle is related to its average of the momentum squared, which is related to its momentum uncertainty.

Solution

To solve this problem, we must be specific about what is meant by “uncertainty of position” and “uncertainty of momentum.” We identify the uncertainty of position

(Δ x)

with the standard deviation of position

(σ_{x})

, and the uncertainty of momentum

(Δ p)

with the standard deviation of momentum

(σ_{p})

. For the Gaussian function, the uncertainty product is

σ_{x} σ_{p} = \frac{ℏ}{2},

where

σ_{x}^{2} = \bar{x^{2}} - {\bar{x}}^{2} and σ_{p}^{2} = \bar{p^{2}} - {\bar{p}}^{2} .

The bar represents an average, so $\bar{x^{2}}$ is the average of $x^{2}$ , while ${\bar{x}}^{2}$ is the square of the average of $x$ , and similarly for $p$ .

The particle is equally likely to be moving left as moving right, so $\bar{p} = 0$ . Also, the uncertainty of position is comparable to the size of the box, so $σ_{x} = L .$ The estimated ground state energy is therefore

E_{0} = E_{Gaussian} = \frac{\bar{p^{2}}}{m} = \frac{σ_{p}^{2}}{2 m} = \frac{1}{2 m} {(\frac{ℏ}{2 σ_{x}})}^{2} = \frac{1}{2 m} {(\frac{ℏ}{2 L})}^{2} = \frac{ℏ^{2}}{8 m L^{2}} .

Multiplying numerator and denominator by $c^{2}$ gives

E_{0} = \frac{{(ℏ c)}^{2}}{8 (m c^{2}) L^{2}} = \frac{{(197.3 eV \cdot nm)}^{2}}{8 (0.511 \cdot 10^{6} eV) {(0.1 nm)}^{2}} = 0.952 eV \approx 1 eV .

Significance

Based on early estimates of the size of a hydrogen atom and the uncertainty principle, the ground-state energy of a hydrogen atom is in the eV range. The ionization energy of an electron in the ground-state energy is approximately 10 eV, so this prediction is roughly confirmed. (Note: The product

ℏ c

is often a useful value in performing calculations in quantum mechanics.)

Energy and Time

Another kind of uncertainty principle concerns uncertainties in simultaneous measurements of the energy of a quantum state and its lifetime,

Δ E Δ t \geq \frac{ℏ}{2},

7.16

where $Δ E$ is the uncertainty in the energy measurement and $Δ t$ is the uncertainty in the lifetime measurement. The energy-time uncertainty principle does not result from a relation of the type expressed by Equation 7.15 for technical reasons beyond this discussion. Nevertheless, the general meaning of the energy-time principle is that a quantum state that exists for only a short time cannot have a definite energy. The reason is that the frequency of a state is inversely proportional to time and the frequency connects with the energy of the state, so to measure the energy with good precision, the state must be observed for many cycles.

To illustrate, consider the excited states of an atom. The finite lifetimes of these states can be deduced from the shapes of spectral lines observed in atomic emission spectra. Each time an excited state decays, the emitted energy is slightly different and, therefore, the emission line is characterized by a distribution of spectral frequencies (or wavelengths) of the emitted photons. As a result, all spectral lines are characterized by spectral widths. The average energy of the emitted photon corresponds to the theoretical energy of the excited state and gives the spectral location of the peak of the emission line. Short-lived states have broad spectral widths and long-lived states have narrow spectral widths.

Example 7.7

Atomic Transitions

An atom typically exists in an excited state for about

Δ t = 10^{−8} s

. Estimate the uncertainty

Δ f

in the frequency of emitted photons when an atom makes a transition from an excited state with the simultaneous emission of a photon with an average frequency of

f = 7.1 \times 10^{14} Hz

. Is the emitted radiation monochromatic?

Strategy

We invert Equation 7.16 to obtain the energy uncertainty

Δ E \approx ℏ / 2 Δ t

and combine it with the photon energy

E = h f

to obtain

Δ f

. To estimate whether or not the emission is monochromatic, we evaluate

Δ f / f

Solution

The spread in photon energies is

Δ E = h Δ f

. Therefore,

\begin{matrix} Δ E & \approx & \frac{ℏ}{2 Δ t} \Rightarrow h Δ f \approx \frac{ℏ}{2 Δ t} \Rightarrow Δ f \approx \frac{1}{4 π Δ t} = \frac{1}{4 π (10^{−8} s)} = 8.0 \times 10^{6} Hz, \\ \frac{Δ f}{f} & = & \frac{8.0 \times 10^{6} Hz}{7.1 \times 10^{14} Hz} = 1.1 \times 10^{−8} . \end{matrix}

Significance

Because the emitted photons have their frequencies within

1.1 \times 10^{−6}

percent of the average frequency, the emitted radiation can be considered monochromatic.

Check Your Understanding 7.4

A sodium atom makes a transition from the first excited state to the ground state, emitting a 589.0-nm photon with energy 2.105 eV. If the lifetime of this excited state is $1.6 \times 10^{−8} s$ , what is the uncertainty in energy of this excited state? What is the width of the corresponding spectral line?