Challenge Problems

90.

Light shows staged with lasers use moving mirrors to swing beams and create colorful effects. Show that a light ray reflected from a mirror changes direction by $2 θ$ when the mirror is rotated by an angle $θ$ .

91.

Consider sunlight entering Earth’s atmosphere at sunrise and sunset—that is, at a $90.0 °$ incident angle. Taking the boundary between nearly empty space and the atmosphere to be sudden, calculate the angle of refraction for sunlight. This lengthens the time the Sun appears to be above the horizon, both at sunrise and sunset. Now construct a problem in which you determine the angle of refraction for different models of the atmosphere, such as various layers of varying density. Your instructor may wish to guide you on the level of complexity to consider and on how the index of refraction varies with air density.

92.

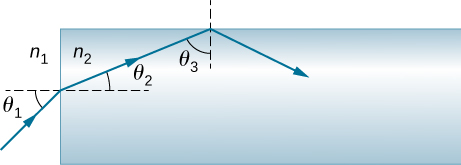
A light ray entering an optical fiber surrounded by air is first refracted and then reflected as shown below. Show that if the fiber is made from crown glass, any incident ray will be totally internally reflected.

$The figure shows light traveling from n 1 and incident onto the left face of a rectangular block of material n 2. The ray is incident at an angle of incidence theta 1, measured relative to the normal to the surface where the ray enters. The angle of refraction is theta 2, again, relative to the normal to the surface. The refracted ray falls onto the upper face of the block and gets totally internally reflected with theta 3 as the angle of incidence.$

93.

A light ray falls on the left face of a prism (see below) at the angle of incidence $θ$ for which the emerging beam has an angle of refraction $θ$ at the right face. Show that the index of refraction n of the glass prism is given by

$n = \frac{sin \frac{1}{2} (α + ϕ)}{sin \frac{1}{2} ϕ}$

where $ϕ$ is the vertex angle of the prism and $α$ is the angle through which the beam has been deviated. If $α = 37.0 °$ and the base angles of the prism are each $50.0 °,$ what is n?

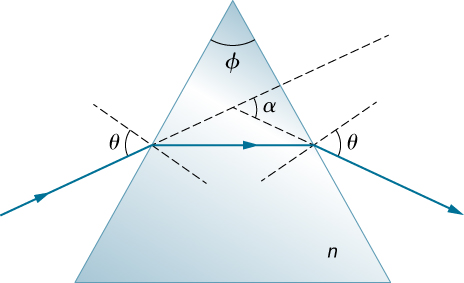
$A light ray falls on the left face of a triangular prism whose upper vertex has an angle of phi and whose index of refraction is n. The angle of incidence of the ray relative to the normal to the left face is theta. The ray refracts in the prism. The refracted ray is horizontal, parallel to the base of the prism. The refracted ray reaches the right face of the prism and refracts as it emerges out of the prism. The emerging ray makes an angle of theta with the normal to the right face.$

94.

If the apex angle $ϕ$ in the previous problem is $20.0 °$ and $n = 1.50$ , what is the value of $α$ ?

95.

The light incident on polarizing sheet $P_{1}$ is linearly polarized at an angle of $30.0 °$ with respect to the transmission axis of $P_{1}$ . Sheet $P_{2}$ is placed so that its axis is parallel to the polarization axis of the incident light, that is, also at $30.0 °$ with respect to $P_{1}$ . (a) What fraction of the incident light passes through $P_{1}$ ? (b) What fraction of the incident light is passed by the combination? (c) By rotating $P_{2}$ , a maximum in transmitted intensity is obtained. What is the ratio of this maximum intensity to the intensity of transmitted light when $P_{2}$ is at $30.0 °$ with respect to $P_{1}$ ?

96.

Prove that if I is the intensity of light transmitted by two polarizing filters with axes at an angle $θ$ and $I ′$ is the intensity when the axes are at an angle $90.0 ° - θ,$ then $I + I^{′} = I_{0},$ the original intensity. (Hint: Use the trigonometric identities $cos 90.0 ° - θ = sin θ$ and ${cos}^{2} θ + {sin}^{2} θ = 1 .)$