9.4 Types of Collisions

Learning Objectives

By the end of this section, you will be able to:

Identify the type of collision
Correctly label a collision as elastic or inelastic
Use kinetic energy along with momentum and impulse to analyze a collision

Although momentum is conserved in all interactions, not all interactions (collisions or explosions) are the same. The possibilities include:

A single object can explode into multiple objects (explosions).
Multiple objects can collide and bounce off each other, called an elastic collision, resulting in the same kinetic energy of the system before and after the collision.
Multiple objects can collide and the system loses kinetic energy, called an inelastic collision. One such case is where the two objects stick together, forming a single object.

It’s useful, therefore, to categorize different types of interactions, according to how the interacting objects move before and after the interaction.

Explosions

The first possibility is that a single object may break apart into two or more pieces. An example of this is a firecracker, or a bow and arrow, or a rocket rising through the air toward space. These can be difficult to analyze if the number of fragments after the collision is more than about three or four; but nevertheless, the total momentum of the system before and after the explosion is identical.

Note that if the object is initially motionless, then the system (which is just the object) has no momentum and no kinetic energy. After the explosion, the net momentum of all the pieces of the object must sum to zero (since the momentum of this closed system cannot change). However, the system will have a great deal of kinetic energy after the explosion, although it had none before. Thus, we see that, although the momentum of the system is conserved in an explosion, the kinetic energy of the system most definitely is not; it increases. This interaction—one object becoming many, with an increase of kinetic energy of the system—is called an explosion.

Where does the energy come from? Does conservation of energy still hold? Yes; some form of potential energy is converted to kinetic energy. In the case of gunpowder burning and pushing out a bullet, chemical potential energy is converted to kinetic energy of the bullet, and of the recoiling gun. For a bow and arrow, it is elastic potential energy in the bowstring.

Inelastic

The second possibility is the reverse: that two or more objects collide with each other and stick together, thus (after the collision) forming one single composite object. The total mass of this composite object is the sum of the masses of the original objects, and the new single object moves with a velocity dictated by the conservation of momentum. However, it turns out again that, although the total momentum of the system of objects remains constant, the kinetic energy doesn’t; but this time, the kinetic energy decreases. This type of collision is called inelastic.

Any collision where the objects stick together will result in the maximum loss of kinetic energy (i.e., $K_{f}$ will be a minimum).

Such a collision is called perfectly inelastic. In the extreme case, multiple objects collide, stick together, and remain motionless after the collision. Since the objects are all motionless after the collision, the final kinetic energy is also zero; therefore, the loss of kinetic energy is a maximum.

If $0 < K_{f} < K_{i}$ , the collision is inelastic.
If $K_{f}$ is the lowest energy, or the energy lost by both objects is the most, the collision is perfectly inelastic (objects stick together).
If $K_{f} = K_{i}$ , the collision is elastic.

Elastic

The extreme case on the other end is if two or more objects approach each other, collide, and bounce off each other, moving away from each other at the same relative speed at which they approached each other. In this case, the total kinetic energy of the system is conserved. Such an interaction is called elastic.

Problem-Solving Strategy

Collisions

A closed system always conserves momentum; it might also conserve kinetic energy, but very often it doesn’t. Energy-momentum problems confined to a plane (as ours are) usually have two unknowns. Generally, this approach works well:

Define a closed system.
Write down the expression for conservation of momentum.
If kinetic energy is conserved, write down the expression for conservation of kinetic energy; if not, write down the expression for the change of kinetic energy.
You now have two equations in two unknowns, which you solve by standard methods.

Example 9.10

Formation of a Deuteron

A proton (mass

1.67 \times 10^{−27} kg

) collides with a neutron (with essentially the same mass as the proton) to form a particle called a deuteron. What is the velocity of the deuteron if it is formed from a proton moving with velocity

7.0 \times 10^{6} m/s

to the right and a neutron moving with velocity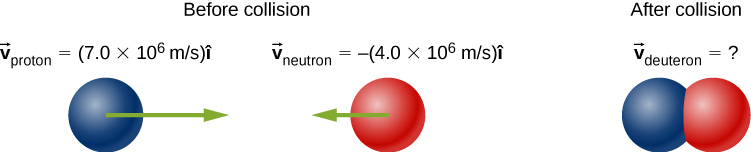

4.0 \times 10^{6} m/s

to the left? Before collision, proton on the left is moving with v sub proton to the right of 7.0 times 10 to the 6 meters per second, and neutron on the right is moving with v sub neutron to the left of -4.0 times 10 to the 6 meters per second. After collision, the proton and deuteron are stuck together, and have unknown v sub deuteron.

Before collision, proton on the left is moving with v sub proton to the right of 7.0 times 10 to the 6 meters per second, and neutron on the right is moving with v sub neutron to the left of -4.0 times 10 to the 6 meters per second. After collision, the proton and deuteron are stuck together, and have unknown v sub deuteron.

Strategy

Define the system to be the two particles. This is a collision, so we should first identify what kind. Since we are told the two particles form a single particle after the collision, this means that the collision is perfectly inelastic. Thus, kinetic energy is not conserved, but momentum is. Thus, we use conservation of momentum to determine the final velocity of the system.

Solution

Treat the two particles as having identical masses M. Use the subscripts p, n, and d for proton, neutron, and deuteron, respectively. This is a one-dimensional problem, so we have

M v_{p} - M v_{n} = 2 M v_{d} .

The masses divide out:

\begin{matrix} v_{p} - v_{n} & = & 2 v_{d} \\ 7.0 \times 10^{6} m/s - 4.0 \times 10^{6} m/s & = & 2 v_{d} \\ v_{d} & = & 1.5 \times 10^{6} m/s. \end{matrix}

The velocity is thus ${\vec{v}}_{d} = (1.5 \times 10^{6} m/s) \hat{i}$ .

Significance

This is essentially how particle colliders like the Large Hadron Collider work: They accelerate particles up to very high speeds (large momenta), but in opposite directions. This maximizes the creation of so-called “daughter particles.”

Example 9.11

Ice Hockey 2

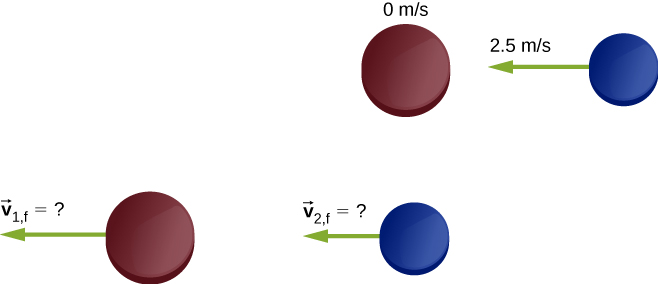
(This is a variation of an earlier example.)

Two ice hockey pucks of different masses are on a flat, horizontal hockey rink. The red puck has a mass of 15 grams, and is motionless; the blue puck has a mass of 12 grams, and is moving at 2.5 m/s to the left. It collides with the motionless red puck (Figure 9.20). If the collision is perfectly elastic, what are the final velocities of the two pucks?

Two hockey pucks are shown. The top diagram shows the puck on the left with 0 meters per second and the puck on the right moving to the left with 2.5 meters per second. The bottom diagram shows the puck on the left moving to the left at unknown v sub 1 f and the puck on the right moving with unknown v sub 2 f.

Figure 9.20 Two different hockey pucks colliding. The top diagram shows the pucks the instant before the collision, and the bottom diagram show the pucks the instant after the collision. The net external force is zero.

Strategy

We’re told that we have two colliding objects, and we’re told their masses and initial velocities; we’re asked for both final velocities. Conservation of momentum seems like a good strategy; define the system to be the two pucks. There is no friction, so we have a closed system. We have two unknowns (the two final velocities), but only one equation. The comment about the collision being perfectly elastic is the clue; it suggests that kinetic energy is also conserved in this collision. That gives us our second equation.

The initial momentum and initial kinetic energy of the system resides entirely and only in the second puck (the blue one); the collision transfers some of this momentum and energy to the first puck.

Solution

Conservation of momentum, in this case, reads

\begin{matrix} p_{i} & = & p_{f} \\ m_{2} v_{2,i} & = & m_{1} v_{1,f} + m_{2} v_{2,f} . \end{matrix}

Conservation of kinetic energy reads

\begin{matrix} K_{i} & = & K_{f} \\ \frac{1}{2} m_{2} v_{2,i}^{2} & = & \frac{1}{2} m_{1} v_{1,f}^{2} + \frac{1}{2} m_{2} v_{2,f}^{2} . \end{matrix}

There are our two equations in two unknowns. The algebra is tedious but not terribly difficult; you definitely should work it through. The solution is

\begin{matrix} v_{1,f} & = & \frac{(m_{1} - m_{2}) v_{1,i} + 2 m_{2} v_{2,i}}{m_{1} + m_{2}} \\ v_{2 f} & = & \frac{(m_{2} - m_{1}) v_{2,i} + 2 m_{1} v_{1,i}}{m_{1} + m_{2}} . \end{matrix}

Substituting with the given numbers where a positive direction is to the left, we obtain

\begin{matrix} v_{1,f} & = & 2.22 \frac{m}{s} \\ v_{2,f} & = & −0.28 \frac{m}{s} . \end{matrix}

Significance

Notice that after the collision, the blue puck is moving to the right; its direction of motion was reversed. The red puck is now moving to the left.

Check Your Understanding 9.7

There is a possible mathematical second to the system of equations solved in this example (because the energy equation is quadratic): $v_{1,f} = 0, v_{2,f} = −2.5 m/s$ . This solution is unacceptable on physical grounds; what’s wrong with it?

Example 9.12

Thor vs. Iron Man

The 2012 movie “The Avengers” has a scene where Iron Man and Thor fight. At the beginning of the fight, Thor throws his hammer at Iron Man, hitting him and throwing him slightly up into the air and against a small tree, which breaks. From the video, Iron Man is standing still when the hammer hits him. The distance between Thor and Iron Man is approximately 10 m, and the hammer takes about 1 s to reach Iron Man after Thor releases it. The tree is about 2 m behind Iron Man, which he hits in about 0.75 s. Also from the video, Iron Man’s trajectory to the tree is very close to horizontal. Assuming Iron Man’s total mass is 200 kg:

Estimate the mass of Thor’s hammer
Estimate how much kinetic energy was lost in this collision

Strategy

After the collision, Thor’s hammer is in contact with Iron Man for the entire time, so this is a perfectly inelastic collision. Thus, with the correct choice of a closed system, we expect momentum is conserved, but not kinetic energy. We use the given numbers to estimate the initial momentum, the initial kinetic energy, and the final kinetic energy. Because this is a one-dimensional problem, we can go directly to the scalar form of the equations.

Solution

First, we posit conservation of momentum. For that, we need a closed system. The choice here is the system (hammer + Iron Man), from the time of collision to the moment just before Iron Man and the hammer hit the tree. Let:
- $M_{H} =$ mass of the hammer
- $M_{I} =$ mass of Iron Man
- $v_{H} =$ velocity of the hammer before hitting Iron Man
- v $=$ combined velocity of Iron Man + hammer after the collision
Again, Iron Man’s initial velocity was zero. Conservation of momentum here reads:
$M_{H} v_{H} = (M_{H} + M_{I}) v .$
We are asked to find the mass of the hammer, so we have
$\begin{matrix} M_{H} v_{H} & = & M_{H} v + M_{I} v \\ M_{H} (v_{H} - v) & = & M_{I} v \\ M_{H} & = & \frac{M_{I} v}{v_{H} - v} \\ = & \frac{(200 kg) (\frac{2 m}{0.75 s})}{10 \frac{m}{s} - (\frac{2 m}{0.75 s})} \\ = & 73 kg. \end{matrix}$
Considering the uncertainties in our estimates, this should be expressed with just one significant figure; thus, MH=7×101kg.
The initial kinetic energy of the system, like the initial momentum, is all in the hammer:
$\begin{matrix} K_{i} & = \frac{1}{2} M_{H} v_{H}^{2} \\ = \frac{1}{2} (70 kg) {(10 m/s)}^{2} \\ = 3500 J. \end{matrix}$
After the collision,
$\begin{matrix} K_{f} & = \frac{1}{2} (M_{H} + M_{I}) v^{2} \\ = \frac{1}{2} (70 kg + 200 kg) {(2.67 m/s)}^{2} \\ = 960 J. \end{matrix}$
Thus, there was a loss of $3500 J - 960 J = 2540 J$ .

Significance

From other scenes in the movie, Thor apparently can control the hammer’s velocity with his mind. It is possible, therefore, that he mentally causes the hammer to maintain its initial velocity of 10 m/s while Iron Man is being driven backward toward the tree. If so, this would represent an external force on our system, so it would not be closed. Thor’s mental control of his hammer is beyond the scope of this book, however.

Example 9.13

Analyzing a Car Crash

At a stoplight, a small car (1200 kg) collides with a motionless large truck (3000 kg). The car comes to an instantaneous stop; the truck slides straight ahead, coming to a stop after sliding 10 meters. The measured coefficient of friction between the truck’s tires and the road was 0.62. How fast was the car moving at the moment of impact?

Strategy

At first it may seem we don’t have enough information to solve this problem. Although we know the initial speed of the truck, we don’t know the speed of the car (indeed, that’s what we’re asked to find), so we don’t know the initial momentum of the system. Similarly, we know the final speed of the car, but not the speed of the truck immediately after impact. The fact that the truck eventually slid to a speed of zero doesn’t help with the final momentum, since an external friction force caused that. Nor can we calculate an impulse, since we don’t know the collision time, or the amount of time the truck slid before stopping. A useful strategy is to impose a restriction on the analysis.

Suppose we define a system consisting of just the car and the truck. The momentum of this system isn’t conserved, because of the friction between the truck and the road. But if we could find the speed of the truck the instant after impact—before friction had any measurable effect on the truck—then we could consider the momentum of the system to be conserved, with that restriction.

Can we find the final speed of the truck? Yes; we invoke the work-energy theorem.

Solution

First, define some variables. Let:

$M_{c} and M_{T}$ be the masses of the car and truck, respectively
$v_{T,i} and v_{T,f}$ be the velocities of the truck before and after the collision, respectively
$v_{c,i} and v_{c,f}$ Z be the velocities of the car before and after the collision, respectively
$K_{i} and K_{f}$ be the kinetic energies of the truck immediately after the collision, and after the truck has stopped sliding (so $K_{f} = 0$ ).
d be the distance the truck slides after the collision before eventually coming to a stop.

Since we actually want the initial speed of the car, and since the car is not part of the work-energy calculation, let’s start with conservation of momentum. For the car + truck system, conservation of momentum reads

\begin{matrix} p_{i} = p_{f} \\ M_{T} v_{T,i} + M_{c} v_{c,i} = M_{T} v_{T,f} + M_{c} v_{c,f} . \end{matrix}

Since the car’s initial velocity was zero, as was the truck’s final velocity, this simplifies to

v_{c,i} = \frac{M_{T}}{M_{c}} v_{T,f} .

So now we need the truck’s speed immediately after impact. Recall that

W = Δ K

where

\begin{matrix} Δ K & = K_{f} - K_{i} \\ = 0 - \frac{1}{2} M_{T} v_{T,f}^{2} . \end{matrix}

Also,

W = \vec{F} \cdot \vec{d} = F d cos θ .

The work is done over the distance the truck slides, which we’ve called d. Equating:

F d cos θ = - \frac{1}{2} M_{T} v_{T,f}^{2} .

Friction is the force on the truck that does the work to stop the sliding. With a level road, the friction force is

F = μ_{k} M_{T} g .

Since the angle between the directions of the friction force vector and the displacement d is $180 °$ , and $cos (180 °) = –1,$ we have

− (μ_{k} M_{T} g) d = - \frac{1}{2} M_{T} v_{T,f}^{2}

(Notice that the truck’s mass divides out; evidently the mass of the truck doesn’t matter.)

Solving for the truck’s speed immediately after the collision gives

v_{T,f} = \sqrt{2 μ_{k} g d} .

Substituting the given numbers:

\begin{matrix} v_{T,f} & = \sqrt{2 (0.62) (9.81 \frac{m}{s^{2}}) (10 m)} \\ = 11.0 m/s . \end{matrix} .

Now we can calculate the initial speed of the car:

v_{T,i} = (\frac{3000 kg}{1200 kg}) (11.0 \frac{m}{s}) = 27.5 m/s .

Significance

This is an example of the type of analysis done by investigators of major car accidents. A great deal of legal and financial consequences depend on an accurate analysis and calculation of momentum and energy.

This collision converted some of the initial kinetic energy to other forms (presumably the deformation of the car and truck and some heat and sound):

K E_{i} = \frac{1}{2} (1200) ({27.5}^{2}) = 4.5 \times 10^{5} J

K E_{f} = \frac{1}{2} (3000) (11^{2}) = 1.8 \times 10^{5} J

Change in kinetic energy = $2.7 \times 10^{5} J$

Check Your Understanding 9.8

Suppose there had been no friction (the collision happened on ice); that would make $μ_{k}$ zero, and thus $v_{c,f} = \sqrt{2 μ_{k} g d} = 0$ , which is obviously wrong. What is the mistake in this conclusion?

Subatomic Collisions and Momentum

Conservation of momentum is crucial to our understanding of atomic and subatomic particles because much of what we know about these particles comes from collision experiments.

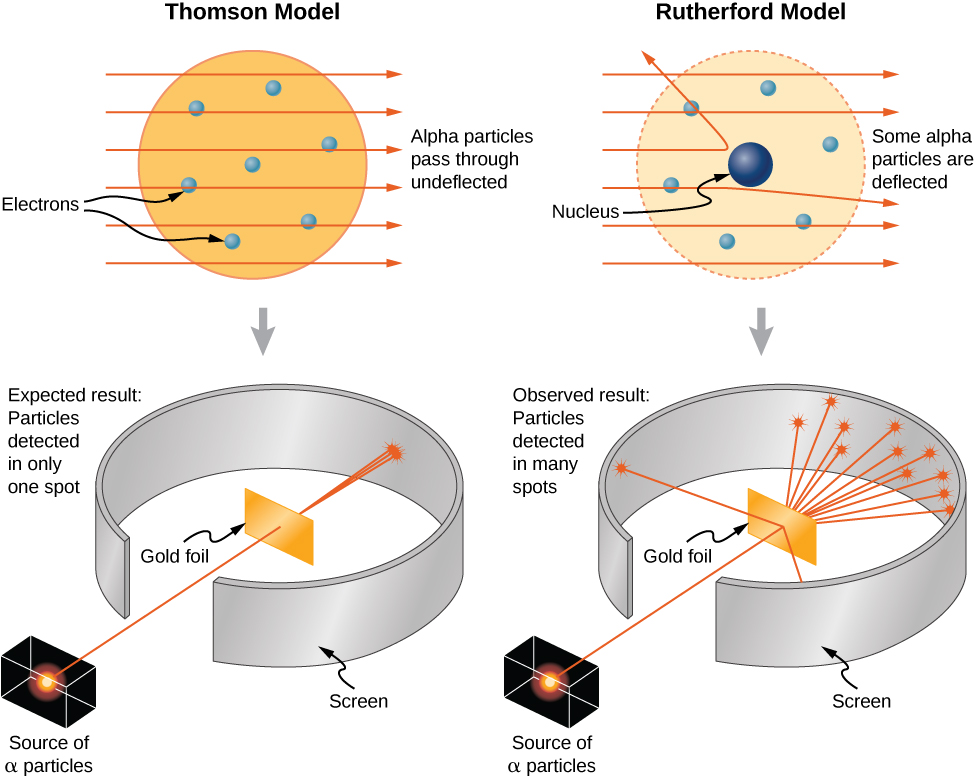
At the beginning of the twentieth century, there was considerable interest in, and debate about, the structure of the atom. It was known that atoms contain two types of electrically charged particles: negatively charged electrons and positively charged protons. (The existence of an electrically neutral particle was suspected, but would not be confirmed until 1932.) The question was, how were these particles arranged in the atom? Were they distributed uniformly throughout the volume of the atom (as J.J. Thomson proposed), or arranged at the corners of regular polygons (which was Gilbert Lewis’ model), or rings of negative charge that surround the positively charged nucleus—rather like the planetary rings surrounding Saturn (as suggested by Hantaro Nagaoka), or something else?

The New Zealand physicist Ernest Rutherford (along with the German physicist Hans Geiger and the British physicist Ernest Marsden) performed the crucial experiment in 1909. They bombarded a thin sheet of gold foil with a beam of high-energy (that is, high-speed) alpha-particles (the nucleus of a helium atom). The alpha-particles collided with the gold atoms, and their subsequent velocities were detected and analyzed, using conservation of momentum and conservation of energy.

If the charges of the gold atoms were distributed uniformly (per Thomson), then the alpha-particles should collide with them and nearly all would be deflected through many angles, all small; the Nagaoka model would produce a similar result. If the atoms were arranged as regular polygons (Lewis), the alpha-particles would deflect at a relatively small number of angles.

What actually happened is that nearly none of the alpha-particles were deflected. Those that were, were deflected at large angles, some close to $180 °$ —those alpha-particles reversed direction completely (Figure 9.21). None of the existing atomic models could explain this. Eventually, Rutherford developed a model of the atom that was much closer to what we now have—again, using conservation of momentum and energy as his starting point.

Illustrations of the Thomson and Rutherford models of the atom and the associated experiments. The Thomson model has electrons, illustrated as small solid balls distributed throughout a large, uniform sphere. Alpha particles pass through undeflected. Several trajectories of alpha particles, incident from the left and travelling horizontally to the right are shown as straight, parallel lines that pass through the atom unchanged. The experiment consists of a collimated source of alpha particles. The beam of particles passes through a gap in a screen that surrounds a gold foil target. The beam passes through the target, spreading a little, but hitting the screen in a small spot on the far side of the screen. The expected result is particles detected in only one spot. The Rutherford model has electrons, illustrated as small solid balls distributed throughout the atom, but the nucleus is a small sphere in the center. Several trajectories of alpha particles, incident from the left and travelling horizontally to the right are shown as straight, parallel lines as they enter the atom. Some pass through unchanged, one is bent slightly away from its original direction, and is bent back at an angle large than 90 degrees. The experiment consists of a collimated source of alpha particles. The beam of particles passes through a gap in a screen that surrounds a gold foil target. The beam passes through the target, most of it passing through but spreading significantly and hitting the screen on the far side over an extended region, and a few of the particles hitting the screen on the same side of foil as the source. The expected result is particles detected in many spots.

Figure 9.21 The Thomson and Rutherford models of the atom. The Thomson model predicted that nearly all of the incident alpha-particles would be scattered and at small angles. Rutherford and Geiger found that nearly none of the alpha particles were scattered, but those few that were deflected did so through very large angles. The results of Rutherford’s experiments were inconsistent with the Thomson model. Rutherford used conservation of momentum and energy to develop a new, and better model of the atom—the nuclear model.