Force and Acceleration

First, what do we mean by a change in motion? The answer is that a change in motion is equivalent to a change in velocity. A change in velocity means, by definition, that there is acceleration. Newton’s first law says that a net external force causes a change in motion; thus, we see that a net external force causes nonzero acceleration.

We defined external force in Forces as force acting on an object or system that originates outside of the object or system. Let’s consider this concept further. An intuitive notion of external is correct—it is outside the system of interest. For example, in Figure 5.10(a), the system of interest is the car plus the person within it. The two forces exerted by the two students are external forces. In contrast, an internal force acts between elements of the system. Thus, the force the person in the car exerts to hang on to the steering wheel is an internal force between elements of the system of interest. Only external forces affect the motion of a system, according to Newton’s first law. (The internal forces cancel each other out, as explained in the next section.) Therefore, we must define the boundaries of the system before we can determine which forces are external. Sometimes, the system is obvious, whereas at other times, identifying the boundaries of a system is more subtle. The concept of a system is fundamental to many areas of physics, as is the correct application of Newton’s laws. This concept is revisited many times in the study of physics.

Figure 5.10 Different forces exerted on the same mass produce different accelerations. (a) Two students push a stalled car. All external forces acting on the car are shown. (b) The forces acting on the car are transferred to a coordinate plane (free-body diagram) for simpler analysis. (c) The tow truck can produce greater external force on the same mass, and thus greater acceleration.

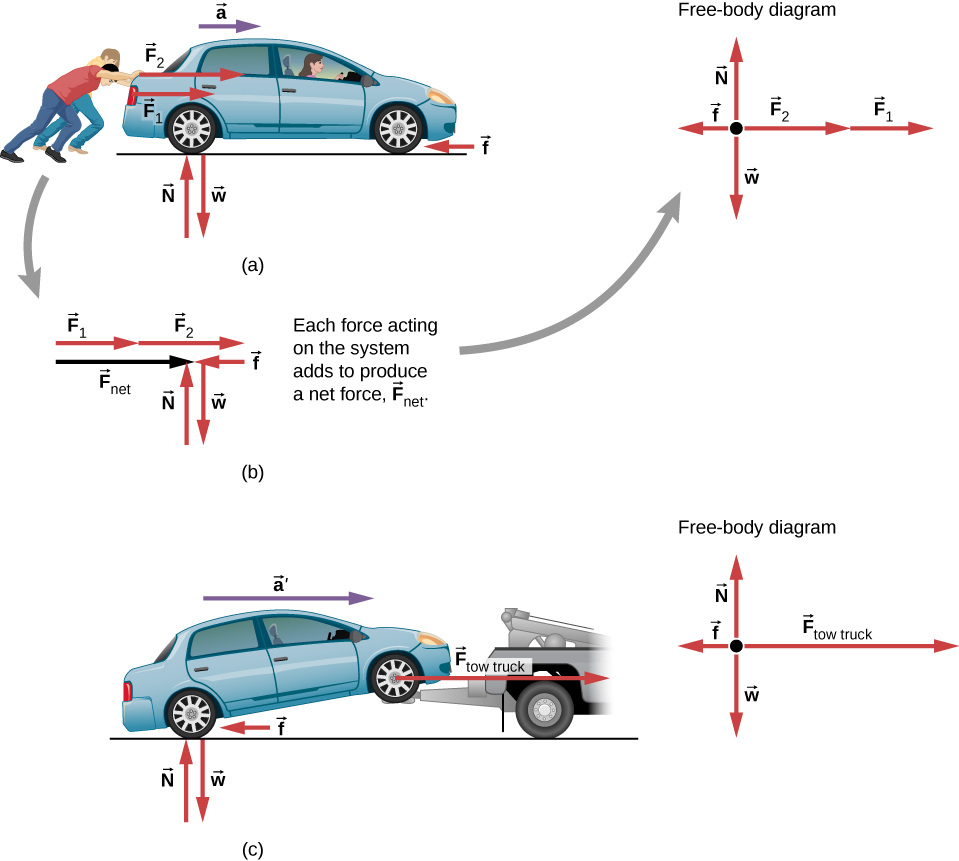
From this example, you can see that different forces exerted on the same mass produce different accelerations. In Figure 5.10(a), the two students push a car with a driver in it. Arrows representing all external forces are shown. The system of interest is the car and its driver. The weight $\overrightarrow{w}$ of the system and the support of the ground $\overrightarrow{N}$ are also shown for completeness and are assumed to cancel (because there was no vertical motion and no imbalance of forces in the vertical direction to create a change in motion). The vector $\overrightarrow{f}$ represents the friction acting on the car, and it acts to the left, opposing the motion of the car. (We discuss friction in more detail in the next chapter.) In Figure 5.10(b), all external forces acting on the system add together to produce the net force ${\overrightarrow{F}}_{\text{net}}.$ The free-body diagram shows all of the forces acting on the system of interest. The dot represents the center of mass of the system. Each force vector extends from this dot. Because there are two forces acting to the right, the vectors are shown collinearly. Finally, in Figure 5.10(c), a larger net external force produces a larger acceleration $(\overrightarrow{a^{\prime }}>\overrightarrow{a})$ when the tow truck pulls the car.

It seems reasonable that acceleration would be directly proportional to and in the same direction as the net external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure 5.10. To obtain an equation for Newton’s second law, we first write the relationship of acceleration $\overrightarrow{a}$ and net external force ${\overrightarrow{F}}_{\text{net}}$ as the proportionality

where the symbol $\propto$ means “proportional to.” (Recall from Forces that the net external force is the vector sum of all external forces and is sometimes indicated as ${\displaystyle \sum \overrightarrow{F}}.$) This proportionality shows what we have said in words—acceleration is directly proportional to net external force. Once the system of interest is chosen, identify the external forces and ignore the internal ones. It is a tremendous simplification to disregard the numerous internal forces acting between objects within the system, such as muscular forces within the students’ bodies, let alone the myriad forces between the atoms in the objects. Still, this simplification helps us solve some complex problems.

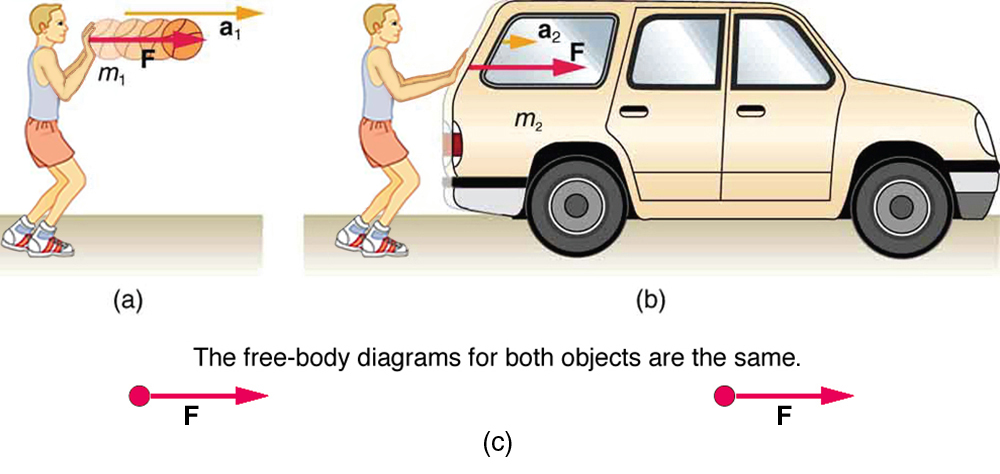
It also seems reasonable that acceleration should be inversely proportional to the mass of the system. In other words, the larger the mass (the inertia), the smaller the acceleration produced by a given force. As illustrated in Figure 5.11, the same net external force applied to a basketball produces a much smaller acceleration when it is applied to an SUV. The proportionality is written as

where m is the mass of the system and a is the magnitude of the acceleration. Experiments have shown that acceleration is exactly inversely proportional to mass, just as it is directly proportional to net external force.

Figure 5.11 The same force exerted on systems of different masses produces different accelerations. (a) A basketball player pushes on a basketball to make a pass. (Ignore the effect of gravity on the ball.) (b) The same player exerts an identical force on a stalled SUV and produces far less acceleration. (c) The free-body diagrams are identical, permitting direct comparison of the two situations. A series of patterns for free-body diagrams will emerge as you do more problems and learn how to draw them in Drawing Free-Body Diagrams.

It has been found that the acceleration of an object depends only on the net external force and the mass of the object. Combining the two proportionalities just given yields Newton’s second law.

The law is a cause-and-effect relationship among three quantities that is not simply based on their definitions. The validity of the second law is based on experimental verification. The free-body diagram, which you will learn to draw in Drawing Free-Body Diagrams, is the basis for writing Newton’s second law.

Example 5.2

What Acceleration Can a Person Produce When Pushing a Lawn Mower?

Suppose that the net external force (push minus friction) exerted on a lawn mower is 51 N (about 11 lb.) parallel to the ground (Figure 5.12). The mass of the mower is 24 kg. What is its acceleration?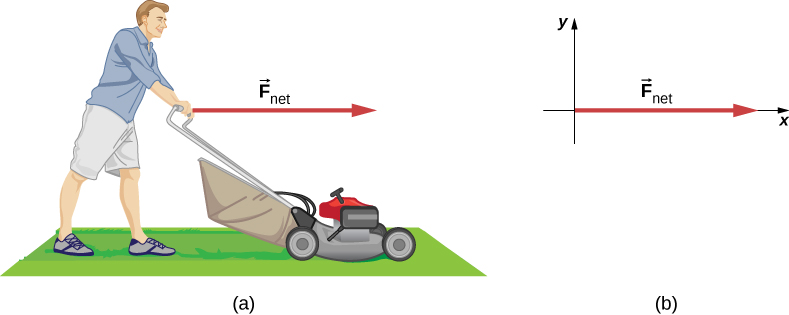

Figure 5.12 (a) The net force on a lawn mower is 51 N to the right. At what rate does the lawn mower accelerate to the right? (b) The free-body diagram for this problem is shown.

Strategy

This problem involves only motion in the horizontal direction; we are also given the net force, indicated by the single vector, but we can suppress the vector nature and concentrate on applying Newton’s second law. Since $F_{\text{net}}$ and m are given, the acceleration can be calculated directly from Newton’s second law as $F_{\text{net}}=ma.$

Solution

The magnitude of the acceleration a is $a=F_{\text{net}}\text{/}m$. Entering known values gives

$$a=\frac{51\text{N}}{24\text{kg}}.$$

Substituting the unit of kilograms times meters per square second for newtons yields

$$a=\frac{51\text{kg}·{\text{m/s}}^2}{24\text{kg}}=2.1{\text{m/s}}^2.$$

Significance

The direction of the acceleration is the same direction as that of the net force, which is parallel to the ground. This is a result of the vector relationship expressed in Newton’s second law, that is, the vector representing net force is the scalar multiple of the acceleration vector. There is no information given in this example about the individual external forces acting on the system, but we can say something about their relative magnitudes. For example, the force exerted by the person pushing the mower must be greater than the friction opposing the motion (since we know the mower moved forward), and the vertical forces must cancel because no acceleration occurs in the vertical direction (the mower is moving only horizontally). The acceleration found is small enough to be reasonable for a person pushing a mower. Such an effort would not last too long, because the person’s top speed would soon be reached.

In the preceding example, we dealt with net force only for simplicity. However, several forces act on the lawn mower. The weight $\overrightarrow{w}$ (discussed in detail in Mass and Weight) pulls down on the mower, toward the center of Earth; this produces a contact force on the ground. The ground must exert an upward force on the lawn mower, known as the normal force $\overrightarrow{N}$, which we define in Common Forces. These forces are balanced and therefore do not produce vertical acceleration. In the next example, we show both of these forces. As you continue to solve problems using Newton’s second law, be sure to show multiple forces.

Example 5.3

Which Force Is Bigger?

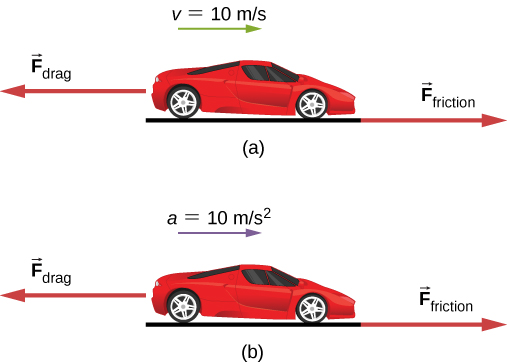
(a) The car shown in Figure 5.13 is moving at a constant speed. Which force is bigger, ${\overrightarrow{F}}_{\text{friction}}$ or ${\overrightarrow{F}}_{\text{drag}}$? Explain.

(b) The same car is now accelerating to the right. Which force is bigger, ${\overrightarrow{F}}_{\text{friction}}$ or ${\overrightarrow{F}}_{\text{drag}}?$ Explain.

Figure 5.13 A car is shown (a) moving at constant speed and (b) accelerating. How do the forces acting on the car compare in each case? (a) What does the knowledge that the car is moving at constant velocity tell us about the net horizontal force on the car compared to the friction force? (b) What does the knowledge that the car is accelerating tell us about the horizontal force on the car compared to the friction force?

Strategy

We must consider Newton’s first and second laws to analyze the situation. We need to decide which law applies; this, in turn, will tell us about the relationship between the forces.

Solution

1. The forces are equal. According to Newton’s first law, if the net force is zero, the velocity is constant.
2. In this case, ${\overrightarrow{F}}_{\text{friction}}$ must be larger than ${\overrightarrow{F}}_{\text{drag}}.$ According to Newton’s second law, a net force is required to cause acceleration.

Significance

These questions may seem trivial, but they are commonly answered incorrectly. For a car or any other object to move, it must be accelerated from rest to the desired speed; this requires that the friction force be greater than the drag force. Once the car is moving at constant velocity, the net force must be zero; otherwise, the car will accelerate (gain speed). To solve problems involving Newton’s laws, we must understand whether to apply Newton’s first law (where ${\displaystyle \sum \overrightarrow{F}}=\overrightarrow{0}$) or Newton’s second law (where ${\displaystyle \sum \overrightarrow{F}}$ is not zero). This will be apparent as you see more examples and attempt to solve problems on your own.

Example 5.4

What Rocket Thrust Accelerates This Sled?

Before space flights carrying astronauts, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets.

Calculate the magnitude of force exerted by each rocket, called its thrust T, for the four-rocket propulsion system shown in Figure 5.14. The sled’s initial acceleration is $49{\text{m/s}}^2$, the mass of the system is 2100 kg, and the force of friction opposing the motion is 650 N.

Figure 5.14 A sled experiences a rocket thrust that accelerates it to the right. Each rocket creates an identical thrust T. The system here is the sled, its rockets, and its rider, so none of the forces between these objects are considered. The arrow representing friction $(\overrightarrow{f})$ is drawn larger than scale.

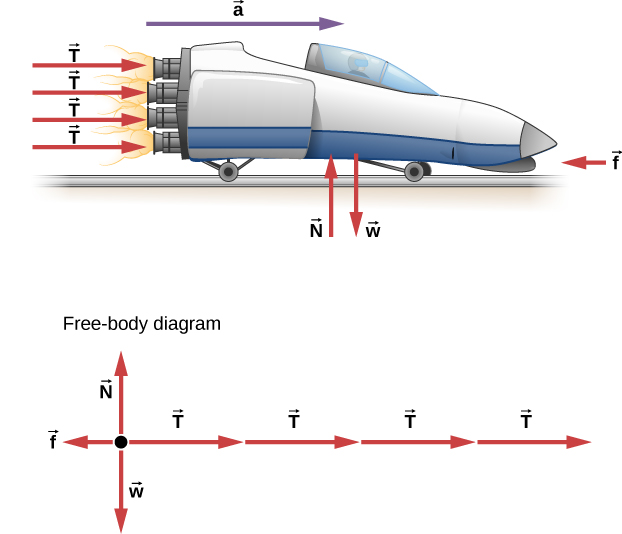
Strategy

Although forces are acting both vertically and horizontally, we assume the vertical forces cancel because there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in Figure 5.14.

Solution

Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. We have defined the direction of the force and acceleration as acting “to the right,” so we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with

$$F_{\text{net}}=ma$$

where $F_{\text{net}}$ is the net force along the horizontal direction. We can see from the figure that the engine thrusts add, whereas friction opposes the thrust. In equation form, the net external force is

$$F_{\text{net}}=4T-f.$$

Substituting this into Newton’s second law gives us

$$F_{\text{net}}=ma=4T-f.$$

Using a little algebra, we solve for the total thrust 4T:

$$4T=ma+f.$$

Substituting known values yields

$$4T=ma+f=\left(2100\text{kg}\right)(49{\text{m}\text{/}\text{s}}^2)+650\text{N}.$$

Therefore, the total thrust is

$$4T=1.0\times {10}^5\text{N},$$

and the individual thrusts are

$$T=\frac{1.0\times {10}^5\text{N}}{4}=2.5\times {10}^4\text{N}.$$

Significance

The numbers are quite large, so the result might surprise you. Experiments such as this were performed in the early 1960s to test the limits of human endurance, and the setup was designed to protect human subjects in jet fighter emergency ejections. Speeds of 1000 km/h were obtained, with accelerations of 45 g’s. (Recall that g, acceleration due to gravity, is $9.80{\text{m/s}}^2$. When we say that acceleration is 45 g’s, it is $45\times 9.8{\text{m/s}}^2,$ which is approximately $440{\text{m/s}}^2$.) Although living subjects are not used anymore, land speeds of 10,000 km/h have been obtained with a rocket sled.

In this example, as in the preceding one, the system of interest is obvious. We see in later examples that choosing the system of interest is crucial—and the choice is not always obvious.

Newton’s second law is more than a definition; it is a relationship among acceleration, force, and mass. It can help us make predictions. Each of those physical quantities can be defined independently, so the second law tells us something basic and universal about nature.

Component Form of Newton’s Second Law

We have developed Newton’s second law and presented it as a vector equation in Equation 5.3. This vector equation can be written as three component equations:

The second law is a description of how a body responds mechanically to its environment. The influence of the environment is the net force ${\overrightarrow{F}}_{\text{net}},$ the body’s response is the acceleration $\overrightarrow{a},$ and the strength of the response is inversely proportional to the mass m. The larger the mass of an object, the smaller its response (its acceleration) to the influence of the environment (a given net force). Therefore, a body’s mass is a measure of its inertia, as we explained in Newton’s First Law.

Example 5.7

Several Forces on a Particle

A particle of mass $m=4.0\text{kg}$ is acted upon by four forces of magnitudes. $F_1=10.0\text{N},F_2=40.0\text{N},F_3=5.0\text{N},\text{and}{F}_4=2.0\text{N}$, with the directions as shown in the free-body diagram in Figure 5.15. What is the acceleration of the particle?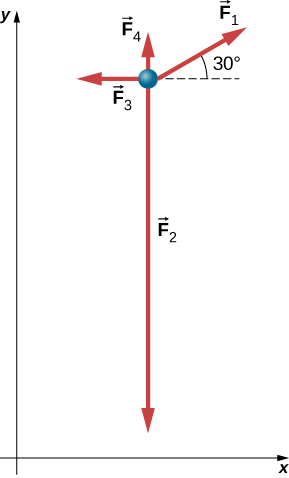

Figure 5.15 Four forces in the xy-plane are applied to a 4.0-kg particle.

Strategy

Because this is a two-dimensional problem, we must use a free-body diagram. First, ${\overrightarrow{F}}_1$ must be resolved into x- and y-components. We can then apply the second law in each direction.

Solution

We draw a free-body diagram as shown in Figure 5.15. Now we apply Newton’s second law. We consider all vectors resolved into x- and y-components:

$$\begin{array}{cccc}{\displaystyle \sum F_x}=m{a}_x\hfill & & & {\displaystyle \sum F_y}=m{a}_y\hfill \\ F_{1x}-F_{3x}=m{a}_x\hfill & & & F_{1y}+F_{4y}-F_{2y}=m{a}_y\hfill \\ F_1\text{cos}30\text{°}-F_{3x}=m{a}_x\hfill & & & F_1\text{sin}30\text{°}+F_{4y}-F_{2y}=m{a}_y\hfill \\ \left(10.0\text{N}\right)\left(\text{cos}30\text{°}\right)-5.0\text{N}=\left(4.0\text{kg}\right)a_x\hfill & & & \left(10.0\text{N}\right)\left(\text{sin}30\text{°}\right)+2.0\text{N}-40.0\text{N}=\left(4.0\text{kg}\right)a_y\hfill \\ a_x=0.92\text{m}\text{/}{\text{s}}^2.\hfill & & & a_y=\mathrm{-8.3}{\text{m}\text{/}\text{s}}^2.\hfill \end{array}$$

Thus, the net acceleration is

$$\overrightarrow{a}=\left(0.92\widehat{i}-8.3\widehat{j}\right)\text{m}\text{/}{\text{s}}^2,$$

which is a vector of magnitude $8.4{\text{m/s}}^2$ directed at $276\text{°}$ to the positive x-axis.

Significance

Numerous examples in everyday life can be found that involve three or more forces acting on a single object, such as cables running from the Golden Gate Bridge or a football player being tackled by three defenders. We can see that the solution of this example is just an extension of what we have already done.

Check Your Understanding 5.5

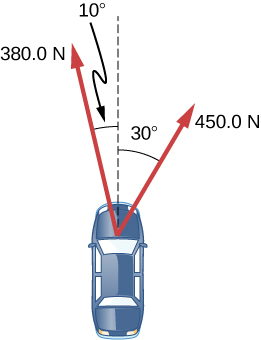
A car has forces acting on it, as shown below. The mass of the car is 1000.0 kg. The road is slick, so friction can be ignored. (a) What is the net force on the car? (b) What is the acceleration of the car?

Newton’s Second Law and Momentum

Newton actually stated his second law in terms of momentum: “The instantaneous rate at which a body’s momentum changes is equal to the net force acting on the body.” (“Instantaneous rate” implies that the derivative is involved.) This can be given by the vector equation

This means that Newton’s second law addresses the central question of motion: What causes a change in motion of an object? Momentum was described by Newton as “quantity of motion,” a way of combining both the velocity of an object and its mass. We devote Linear Momentum and Collisions to the study of momentum.

For now, it is sufficient to define momentum $\overrightarrow{p}$ as the product of the mass of the object m and its velocity $\overrightarrow{v}$:

Since velocity is a vector, so is momentum.

It is easy to visualize momentum. A train moving at 10 m/s has more momentum than one that moves at 2 m/s. In everyday life, we speak of one sports team as “having momentum” when they score points against the opposing team.

If we substitute Equation 5.7 into Equation 5.6, we obtain

When m is constant, we have

Thus, we see that the momentum form of Newton’s second law reduces to the form given earlier in this section.