9.5 Collisions in Multiple Dimensions

It is far more common for collisions to occur in two dimensions; that is, the angle between the initial velocity vectors is neither zero nor $180\text{°}$. Let’s see what complications arise from this.

The first idea we need is that momentum is a vector; like all vectors, it can be expressed as a sum of perpendicular components (usually, though not always, an x-component and a y-component, and a z-component if necessary). Thus, when we write down the statement of conservation of momentum for a problem, our momentum vectors can be, and usually will be, expressed in component form.

The second idea we need comes from the fact that momentum is related to force:

Expressing both the force and the momentum in component form,

Remember, these equations are simply Newton’s second law, in vector form and in component form. We know that Newton’s second law is true in each direction, independently of the others. It follows therefore (via Newton’s third law) that conservation of momentum is also true in each direction independently.

These two ideas motivate the solution to two-dimensional problems: We write down the expression for conservation of momentum twice: once in the x-direction and once in the y-direction.

This procedure is shown graphically in Figure 9.22.

Figure 9.22 (a) For two-dimensional momentum problems, break the initial momentum vectors into their x- and y-components. (b) Add the x- and y-components together separately. This gives you the x- and y-components of the final momentum, which are shown as red dashed vectors. (c) Adding these components together gives the final momentum.

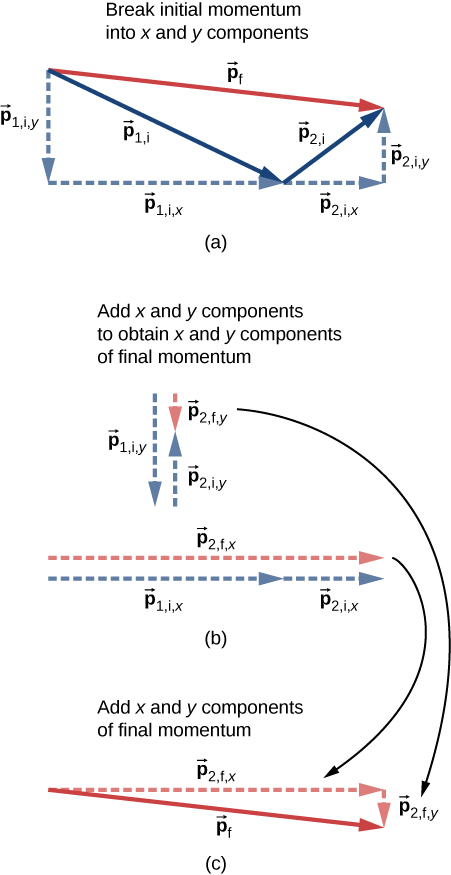
We solve each of these two component equations independently to obtain the x- and y-components of the desired velocity vector:

(Here, m represents the total mass of the system.) Finally, combine these components using the Pythagorean theorem,

Example 9.14

Traffic Collision

A small car of mass 1200 kg traveling east at 60 km/hr collides at an intersection with a truck of mass 3000 kg that is traveling due north at 40 km/hr (Figure 9.23). The two vehicles are locked together. What is the velocity of the combined wreckage?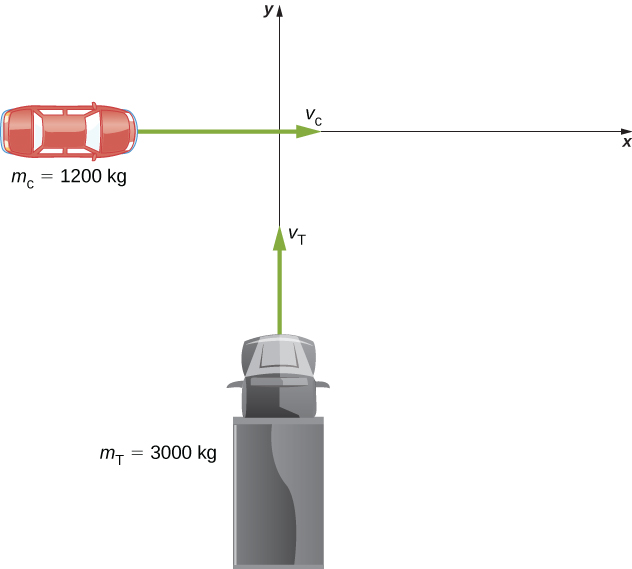

Figure 9.23 A large truck moving north is about to collide with a small car moving east. The final momentum vector has both x- and y-components.

Strategy

First off, we need a closed system. The natural system to choose is the (car + truck), but this system is not closed; friction from the road acts on both vehicles. We avoid this problem by restricting the question to finding the velocity at the instant just after the collision, so that friction has not yet had any effect on the system. With that restriction, momentum is conserved for this system.

Since there are two directions involved, we do conservation of momentum twice: once in the x-direction and once in the y-direction.

Solution

Before the collision the total momentum is

$$\overrightarrow{p}=m_{\text{c}}{\overrightarrow{v}}_{\text{c}}+m_{\text{T}}{\overrightarrow{v}}_{\text{T}}.$$

After the collision, the wreckage has momentum

$$\overrightarrow{p}=\left(m_{\text{c}}+m_{\text{T}}\right){\overrightarrow{v}}_w.$$

Since the system is closed, momentum must be conserved, so we have

$$m_{\text{c}}{\overrightarrow{v}}_c+m_{\text{T}}{\overrightarrow{v}}_{\text{T}}=\left(m_{\text{c}}+m_{\text{T}}\right){\overrightarrow{v}}_w.$$

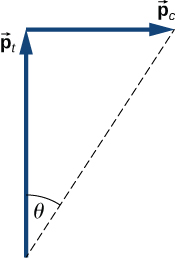
We have to be careful; the two initial momenta are not parallel. We must add vectorially (Figure 9.24).

Figure 9.24 Graphical addition of momentum vectors. Notice that, although the car’s velocity is larger than the truck’s, its momentum is smaller.

If we define the +x-direction to point east and the +y-direction to point north, as in the figure, then (conveniently),

$$\begin{array}{ccc}\hfill {\overrightarrow{p}}_{\text{c}}& =\hfill & p_{\text{c}}\widehat{i}=m_{\text{c}}{v}_{\text{c}}\widehat{i}\hfill \\ \hfill {\overrightarrow{p}}_{\text{T}}& =\hfill & p_{\text{T}}\widehat{j}=m_{\text{T}}{v}_{\text{T}}\widehat{j}.\hfill \end{array}$$

Therefore, in the x-direction:

$$\begin{array}{ccc}\hfill m_{\text{c}}{v}_{\text{c}}& =\hfill & \left(m_{\text{c}}+m_{\text{T}}\right)v_{\text{w},x}\hfill \\ \hfill v_{\text{w},x}& =\hfill & \left(\frac{m_{\text{c}}}{m_{\text{c}}+m_{\text{T}}}\right)v_{\text{c}}\hfill \end{array}$$

and in the y-direction:

$$\begin{array}{ccc}\hfill m_{\text{T}}{v}_{\text{T}}& =\hfill & \left(m_{\text{c}}+m_{\text{T}}\right)v_{\text{w},y}\hfill \\ \hfill v_{\text{w},y}& =\hfill & \left(\frac{m_{\text{T}}}{m_{\text{c}}+m_{\text{T}}}\right)v_{\text{T}}.\hfill \end{array}$$

Applying the Pythagorean theorem gives

$$\begin{array}{cc}\hfill \left|{\overrightarrow{v}}_w\right|& =\sqrt{{\left[\left(\frac{m_{\text{c}}}{m_{\text{c}}+m_t}\right)v_{\text{c}}\right]}^2+{\left[\left(\frac{m_t}{m_{\text{c}}+m_t}\right)v_t\right]}^2}\hfill \\ & =\sqrt{{\left[\left(\frac{1200\text{kg}}{4200\text{kg}}\right)\left(16.67\frac{\text{m}}{\text{s}}\right)\right]}^2+{\left[\left(\frac{3000\text{kg}}{4200\text{kg}}\right)\left(11.1\frac{\text{m}}{\text{s}}\right)\right]}^2}\hfill \\ & =\sqrt{{\left(4.76\frac{\text{m}}{\text{s}}\right)}^2+{\left(7.93\frac{\text{m}}{\text{s}}\right)}^2}\hfill \\ & =9.25\frac{\text{m}}{\text{s}}\approx 33.3\frac{\text{km}}{\text{hr}}.\hfill \end{array}$$

As for its direction, using the angle shown in the figure,

$$\theta ={\text{tan}}^{\mathrm{-1}}\left(\frac{v_{\text{w},x}}{v_{\text{w},y}}\right)={\text{tan}}^{\mathrm{-1}}\left(\frac{7.93\text{m/s}}{4.76\text{m/s}}\right)=59\text{°}.$$

This angle is east of north, or $31\text{°}$ counterclockwise from the +x-direction.

Significance

As a practical matter, accident investigators usually work in the “opposite direction”; they measure the distance of skid marks on the road (which gives the stopping distance) and use the work-energy theorem along with conservation of momentum to determine the speeds and directions of the cars prior to the collision. We saw that analysis in an earlier section.

Example 9.15

Exploding Scuba Tank

A common scuba tank is an aluminum cylinder that weighs 31.7 pounds empty (Figure 9.25). When full of compressed air, the internal pressure is between 2500 and 3000 psi (pounds per square inch). Suppose such a tank, which had been sitting motionless, suddenly explodes into three pieces. The first piece, weighing 10 pounds, shoots off horizontally at 235 miles per hour; the second piece (7 pounds) shoots off at 172 miles per hour, also in the horizontal plane, but at a $19\text{°}$ angle to the first piece. What is the mass and initial velocity of the third piece? (Do all work, and express your final answer, in SI units.)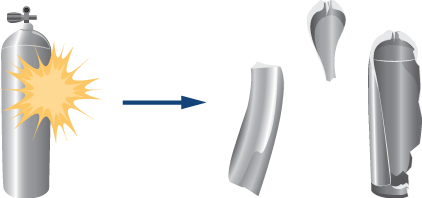

Figure 9.25 A scuba tank explodes into three pieces.

Strategy

To use conservation of momentum, we need a closed system. If we define the system to be the scuba tank, this is not a closed system, since gravity is an external force. However, the problem asks for just the initial velocity of the third piece, so we can neglect the effect of gravity and consider the tank by itself as a closed system. Notice that, for this system, the initial momentum vector is zero.

We choose a coordinate system where all the motion happens in the xy-plane. We then write down the equations for conservation of momentum in each direction, thus obtaining the x- and y-components of the momentum of the third piece, from which we obtain its magnitude (via the Pythagorean theorem) and its direction. Finally, dividing this momentum by the mass of the third piece gives us the velocity.

Solution

First, let’s get all the conversions to SI units out of the way:

$$\begin{array}{}\\ \\ 31.7\text{lb}\times \frac{1\text{kg}}{2.2\text{lb}}\to 14.4\text{kg}\hfill \\ 10\text{lb}\to 4.5\text{kg}\hfill \\ 235\frac{\text{miles}}{\text{hour}}\times \frac{1\text{hour}}{3600\text{s}}\times \frac{1609\text{m}}{\text{mile}}=105\frac{\text{m}}{\text{s}}\hfill \\ 7\text{lb}\to 3.2\text{kg}\hfill \\ 172\frac{\text{mile}}{\text{hour}}=77\frac{\text{m}}{\text{s}}\hfill \\ m_3=14.4\text{kg}-\left(4.5\text{kg}+3.2\text{kg}\right)=6.7\text{kg.}\hfill \end{array}$$

Now apply conservation of momentum in each direction.

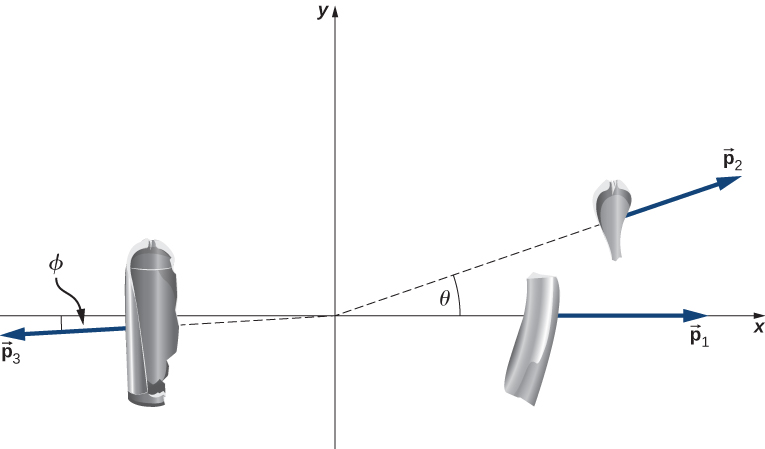
x-direction:

$$\begin{array}{ccc}\hfill p_{\text{f,}x}& =\hfill & p_{\text{0,}x}\hfill \\ \hfill p_{\text{1,}x}+p_{\text{2,}x}+p_{\text{3,}x}& =\hfill & 0\hfill \\ \hfill m_1{v}_{\text{1,}x}+m_2{v}_{\text{2,}x}+p_{\text{3,}x}& =\hfill & 0\hfill \\ \hfill p_{\text{3,}x}& =\hfill & \text{−}{m}_1{v}_{\text{1,}x}-m_2{v}_{\text{2,}x}\hfill \end{array}$$

y-direction:

$$\begin{array}{ccc}\hfill p_{\text{f,}y}& =\hfill & p_{\text{0,}y}\hfill \\ \hfill p_{\text{1,}y}+p_{\text{2,}y}+p_{\text{3,}y}& =\hfill & 0\hfill \\ \hfill m_1{v}_{\text{1,}y}+m_2{v}_{\text{2,}y}+p_{\text{3,}y}& =\hfill & 0\hfill \\ \hfill p_{\text{3,}y}& =\hfill & \text{−}{m}_1{v}_{\text{1,}y}-m_2{v}_{\text{2,}y}\hfill \end{array}$$

From our chosen coordinate system, we write the x-components as

$$\begin{array}{cc}\hfill p_{3,x}& =\text{−}{m}_1{v}_1-m_2{v}_2\text{cos}\theta \hfill \\ & =\text{−}\left(4.5\text{kg}\right)\left(105\frac{\text{m}}{\text{s}}\right)-\left(3.2\text{kg}\right)\left(77\frac{\text{m}}{\text{s}}\right)\text{cos}\left(19\text{°}\right)\hfill \\ & =\mathrm{-705}\frac{\text{kg}·\text{m}}{\text{s}}.\hfill \end{array}$$

For the y-direction, we have

$$\begin{array}{cc}\hfill p_{3y}& =0-m_2{v}_2\text{sin}\theta \hfill \\ & =\text{−}\left(3.2\text{kg}\right)\left(77\frac{\text{m}}{\text{s}}\right)\text{sin}\left(19\text{°}\right)\hfill \\ & =\mathrm{-80.2}\frac{\text{kg}·\text{m}}{\text{s}}.\hfill \end{array}$$

This gives the magnitude of $p_3$:

$$\begin{array}{cc}\hfill p_3& =\sqrt{p_{\text{3,}x}^2+p_{\text{3,}y}^2}\hfill \\ & =\sqrt{{\left(\mathrm{-705}\frac{\text{kg}·\text{m}}{\text{s}}\right)}^2+\left(\mathrm{-80.2}\frac{\text{kg}·\text{m}}{\text{s}}\right)}\hfill \\ & =710\frac{\text{kg}·\text{m}}{\text{s}}.\hfill \end{array}$$

The velocity of the third piece is therefore

$$v_3=\frac{p_3}{m_3}=\frac{710\frac{\text{kg}·\text{m}}{\text{s}}}{6.7\text{kg}}=106\frac{\text{m}}{\text{s}}.$$

The direction of its velocity vector is the same as the direction of its momentum vector:

$$\varphi ={\text{tan}}^{\mathrm{-1}}\left(\frac{p_{\text{3,}y}}{p_{\text{3,}x}}\right)={\text{tan}}^{\mathrm{-1}}\left(\frac{80.2\frac{\text{kg}·\text{m}}{\text{s}}}{705\frac{\text{kg}·\text{m}}{\text{s}}}\right)=6.49\text{°}.$$

Because $\varphi$ is below the $\text{−}x$-axis, the actual angle is $183.5\text{°}$ from the +x-direction.

Significance

The enormous velocities here are typical; an exploding tank of any compressed gas can easily punch through the wall of a house and cause significant injury, or death. Fortunately, such explosions are extremely rare, on a percentage basis.