13.3 Motional Emf
Learning Objectives
By the end of this section, you will be able to:
- Determine the magnitude of an induced emf in a wire moving at a constant speed through a magnetic field
- Discuss examples that use motional emf, such as a rail gun and a tethered satellite
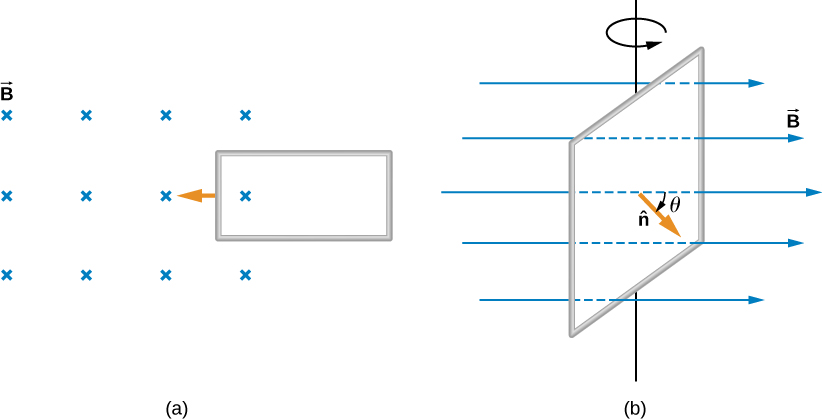
Magnetic flux depends on three factors: the strength of the magnetic field, the area through which the field lines pass, and the orientation of the field with the surface area. If any of these quantities varies, a corresponding variation in magnetic flux occurs. So far, we’ve only considered flux changes due to a changing field. Now we look at another possibility: a changing area through which the field lines pass including a change in the orientation of the area.
Two examples of this type of flux change are represented in Figure 13.11. In part (a), the flux through the rectangular loop increases as it moves into the magnetic field, and in part (b), the flux through the rotating coil varies with the angle .
Now let’s look at a conducting rod pulled in a circuit, changing magnetic flux. The area enclosed by the circuit ‘MNOP’ of Figure 13.12 is lx and is perpendicular to the magnetic field, so we can simplify the integration of Equation 13.1 into a multiplication of magnetic field and area. The magnetic flux through the open surface is therefore
Since B and l are constant and the velocity of the rod is we can now restate Faraday’s law, Equation 13.2, for the magnitude of the emf in terms of the moving conducting rod as
The current induced in the circuit is the emf divided by the resistance or
Furthermore, the direction of the induced emf satisfies Lenz’s law, as you can verify by inspection of the figure.
This calculation of motionally induced emf is not restricted to a rod moving on conducting rails. With as the starting point, it can be shown that holds for any change in flux caused by the motion of a conductor. We saw in Faraday’s Law that the emf induced by a time-varying magnetic field obeys this same relationship, which is Faraday’s law. Thus Faraday’s law holds for all flux changes, whether they are produced by a changing magnetic field, by motion, or by a combination of the two.
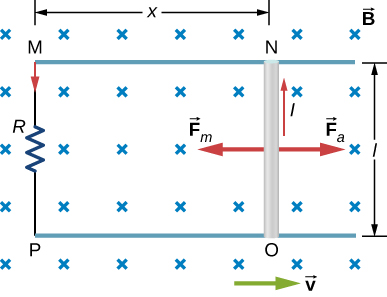
From an energy perspective, produces power and the resistor dissipates power . Since the rod is moving at constant velocity, the applied force must balance the magnetic force on the rod when it is carrying the induced current I. Thus the power produced is
The power dissipated is
In satisfying the principle of energy conservation, the produced and dissipated powers are equal.
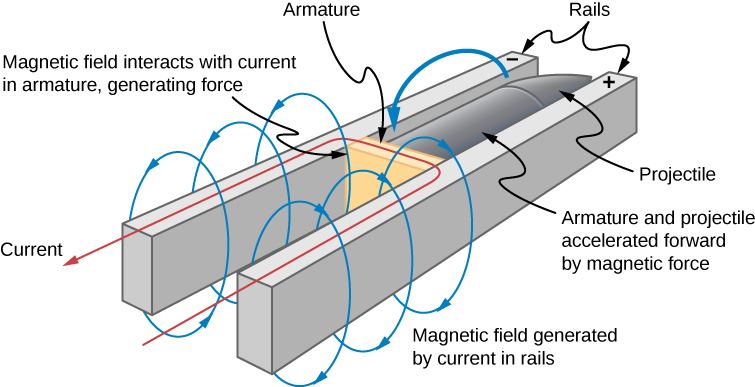
This principle can be seen in the operation of a rail gun. A rail gun is an electromagnetic projectile launcher that uses an apparatus similar to Figure 13.12 and is shown in schematic form in Figure 13.13. The conducting rod is replaced with a projectile or weapon to be fired. So far, we’ve only heard about how motion causes an emf. In a rail gun, the optimal shutting off/ramping down of a magnetic field decreases the flux in between the rails, causing a current to flow in the rod (armature) that holds the projectile. This current through the armature experiences a magnetic force and is propelled forward. Rail guns, however, are not used widely in the military due to the high cost of production and high currents: Nearly one million amps is required to produce enough energy for a rail gun to be an effective weapon.
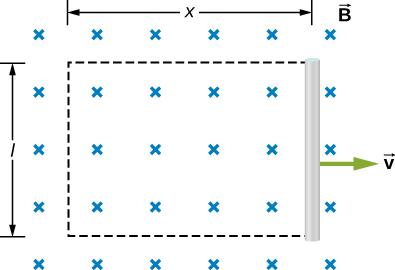
We can calculate a motionally induced emf with Faraday’s law even when an actual closed circuit is not present. We simply imagine an enclosed area whose boundary includes the moving conductor, calculate , and then find the emf from Faraday’s law. For example, we can let the moving rod of Figure 13.14 be one side of the imaginary rectangular area represented by the dashed lines. The area of the rectangle is lx, so the magnetic flux through it is Differentiating this equation, we obtain
which is identical to the potential difference between the ends of the rod that we determined earlier.
Motional emfs in Earth’s weak magnetic field are not ordinarily very large, or we would notice voltage along metal rods, such as a screwdriver, during ordinary motions. For example, a simple calculation of the motional emf of a 1.0-m rod moving at 3.0 m/s perpendicular to the Earth’s field gives
This small value is consistent with experience. There is a spectacular exception, however. In 1992 and 1996, attempts were made with the space shuttle to create large motional emfs. The tethered satellite was to be let out on a 20-km length of wire, as shown in Figure 13.15, to create a 5-kV emf by moving at orbital speed through Earth’s field. This emf could be used to convert some of the shuttle’s kinetic and potential energy into electrical energy if a complete circuit could be made. To complete the circuit, the stationary ionosphere was to supply a return path through which current could flow. (The ionosphere is the rarefied and partially ionized atmosphere at orbital altitudes. It conducts because of the ionization. The ionosphere serves the same function as the stationary rails and connecting resistor in Figure 13.13, without which there would not be a complete circuit.) Drag on the current in the cable due to the magnetic force does the work that reduces the shuttle’s kinetic and potential energy, and allows it to be converted into electrical energy. Both tests were unsuccessful. In the first, the cable hung up and could only be extended a couple of hundred meters; in the second, the cable broke when almost fully extended. Example 13.4 indicates feasibility in principle.
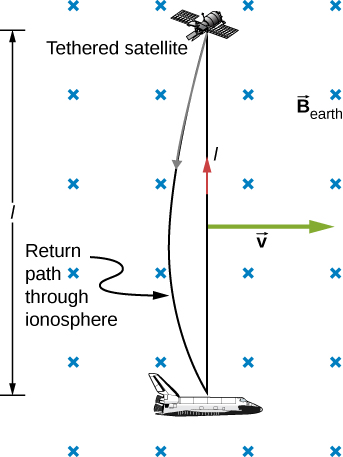
Example 13.4
Calculating the Large Motional Emf of an Object in Orbit
Calculate the motional emf induced along a 20.0-km conductor moving at an orbital speed of 7.80 km/s perpendicular to Earth’s magnetic field.Strategy
This is a great example of using the equation motionalSolution
Entering the given values into givesSignificance
The value obtained is greater than the 5-kV measured voltage for the shuttle experiment, since the actual orbital motion of the tether is not perpendicular to Earth’s field. The 7.80-kV value is the maximum emf obtained when and soExample 13.5
A Metal Rod Rotating in a Magnetic Field
Part (a) of Figure 13.16 shows a metal rod OS that is rotating in a horizontal plane around point O. The rod slides along a wire that forms a circular arc PST of radius r. The system is in a constant magnetic field that is directed out of the page. (a) If you rotate the rod at a constant angular velocity , what is the current I in the closed loop OPSO? Assume that the resistor R furnishes all of the resistance in the closed loop. (b) Calculate the work per unit time that you do while rotating the rod and show that it is equal to the power dissipated in the resistor.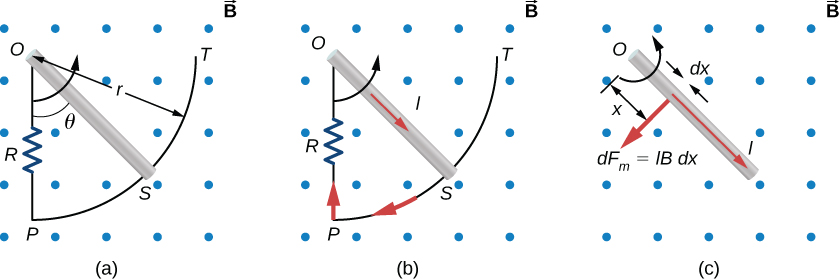
Strategy
The magnetic flux is the magnetic field times the area of the quarter circle or When finding the emf through Faraday’s law, all variables are constant in time but , with To calculate the work per unit time, we know this is related to the torque times the angular velocity. The torque is calculated by knowing the force on a rod and integrating it over the length of the rod.Solution
- From geometry, the area of the loop OPSO is Hence, the magnetic flux through the loop is Differentiating with respect to time and using we have When divided by the resistance R of the loop, this yields for the magnitude of the induced current As increases, so does the flux through the loop due to To counteract this increase, the magnetic field due to the induced current must be directed into the page in the region enclosed by the loop. Therefore, as part (b) of Figure 13.16 illustrates, the current circulates clockwise.
- You rotate the rod by exerting a torque on it. Since the rod rotates at constant angular velocity, this torque is equal and opposite to the torque exerted on the current in the rod by the original magnetic field. The magnetic force on the infinitesimal segment of length dx shown in part (c) of Figure 13.16 is so the magnetic torque on this segment is The net magnetic torque on the rod is then The torque that you exert on the rod is equal and opposite to and the work that you do when the rod rotates through an angle is Hence, the work per unit time that you do on the rod is where we have substituted for I. The power dissipated in the resistor is , which can be written as Therefore, we see that Hence, the power dissipated in the resistor is equal to the work per unit time done in rotating the rod.
Significance
An alternative way of looking at the induced emf from Faraday’s law is to integrate in space instead of time. The solution, however, would be the same. The motional emf isThe velocity can be written as the angular velocity times the radius and the differential length written as dr. Therefore,
which is the same solution as before.
Example 13.6
A Rectangular Coil Rotating in a Magnetic Field
A rectangular coil of area A and N turns is placed in a uniform magnetic field as shown in Figure 13.17. The coil is rotated about the z-axis through its center at a constant angular velocity Obtain an expression for the induced emf in the coil.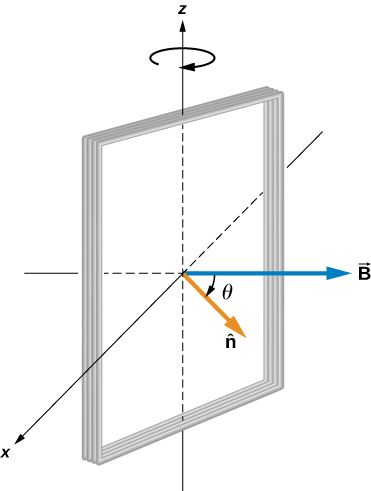
Strategy
According to the diagram, the angle between the perpendicular to the surface () and the magnetic field is . The dot product of simplifies to only the component of the magnetic field, namely where the magnetic field projects onto the unit area vector . The magnitude of the magnetic field and the area of the loop are fixed over time, which makes the integration simplify quickly. The induced emf is written out using Faraday’s law.Solution
When the coil is in a position such that its normal vector makes an angle with the magnetic field the magnetic flux through a single turn of the coil isFrom Faraday’s law, the emf induced in the coil is
The constant angular velocity is The angle represents the time evolution of the angular velocity or . This is changes the function to time space rather than . The induced emf therefore varies sinusoidally with time according to
where
Significance
If the magnetic field strength or area of the loop were also changing over time, these variables wouldn’t be able to be pulled out of the time derivative to simplify the solution as shown. This example is the basis for an electric generator, as we will give a full discussion in Electric Generators and Back Emf.Check Your Understanding 13.4
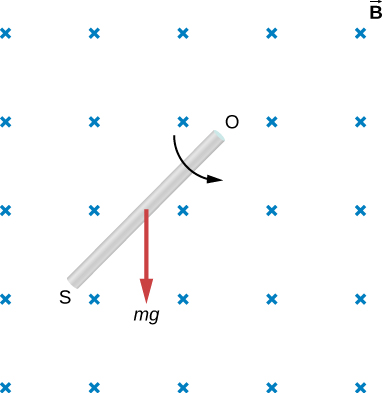
Shown below is a rod of length l that is rotated counterclockwise around the axis through O by the torque due to Assuming that the rod is in a uniform magnetic field , what is the emf induced between the ends of the rod when its angular velocity is ? Which end of the rod is at a higher potential?
Check Your Understanding 13.5
A rod of length 10 cm moves at a speed of 10 m/s perpendicularly through a 1.5-T magnetic field. What is the potential difference between the ends of the rod?