Angular Velocity

Uniform circular motion (discussed previously in Motion in Two and Three Dimensions) is motion in a circle at constant speed. Although this is the simplest case of rotational motion, it is very useful for many situations, and we use it here to introduce rotational variables.

In Figure 10.2, we show a particle moving in a circle. The coordinate system is fixed and serves as a frame of reference to define the particle’s position. Its position vector from the origin of the circle to the particle sweeps out the angle $\theta$, which increases in the counterclockwise direction as the particle moves along its circular path. The angle $\theta$ is called the angular position of the particle. As the particle moves in its circular path, it also traces an arc length s. The particle may complete more than one revolution around the circle, and so the angle $\theta$ may be greater than $2\pi$, and the arc length s may be greater than the circumference, $2\pi r$.

Figure 10.2 A particle follows a circular path. As it moves counterclockwise, it sweeps out a positive angle $\theta$ with respect to the x-axis and traces out an arc length s.

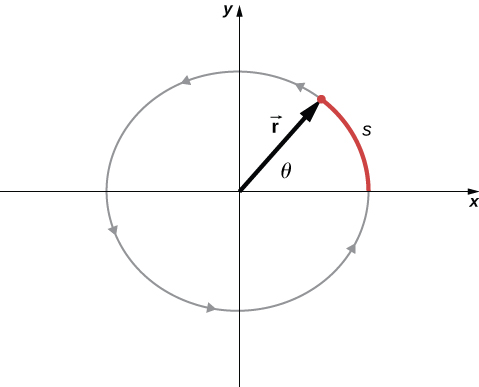
The angle is related to the radius of the circle and the arc length by

The angle $\theta$, the angular position of the particle along its path, has units of radians (rad). There are $2\pi$ radians in $360\text{°}.$ Note that the radian measure is a ratio of length measurements, and therefore is a dimensionless quantity. As the particle moves along its circular path, its angular position changes and it undergoes angular displacements $\text{Δ}\theta .$

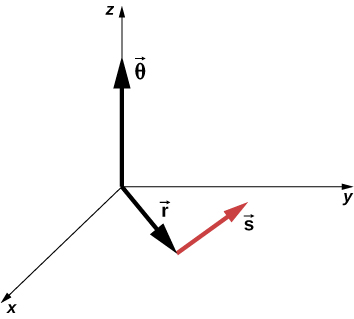
We can assign vectors to the quantities in Equation 10.1. The angle $\overrightarrow{\theta }$ is a vector out of the page in Figure 10.2. The angular position vector $\overrightarrow{r}$ and the arc length $\overrightarrow{s}$ both lie in the plane of the page. These three vectors are related to each other by

That is, the arc length is the cross product of the angle vector and the position vector, as shown in Figure 10.3.

Figure 10.3 The angle vector points along the z-axis and the position vector and arc length vector both lie in the xy-plane. We see that $\overrightarrow{s}=\overrightarrow{\theta }\times \overrightarrow{r}$. All three vectors are perpendicular to each other.

The magnitude of the angular velocity, denoted by $\omega$, is the time rate of change of the angle $\theta$ as the particle moves in its circular path. The instantaneous angular velocity is defined as the limit in which $\text{Δ}t\to 0$ in the average angular velocity $\bar{\omega }=\frac{\text{Δ}\theta }{\text{Δ}t}$:

where $\theta$ is the angle of rotation (Figure 10.2). The units of angular velocity are radians per second (rad/s). Angular velocity can also be referred to as the rotation rate in radians per second. In many situations, we are given the rotation rate in revolutions/s or cycles/s. To find the angular velocity, we must multiply revolutions/s by $2\pi$, since there are $2\pi$ radians in one complete revolution. Since the direction of a positive angle in a circle is counterclockwise, we take counterclockwise rotations as being positive and clockwise rotations as negative.

We can see how angular velocity is related to the tangential speed of the particle by differentiating Equation 10.1 with respect to time. We rewrite Equation 10.1 as

Taking the derivative with respect to time and noting that the radius r is a constant, we have

where $\theta \frac{dr}{dt}=0$. Here $\frac{ds}{dt}$ is just the tangential speed $v_{\text{t}}$ of the particle in Figure 10.2. Thus, by using Equation 10.3, we arrive at

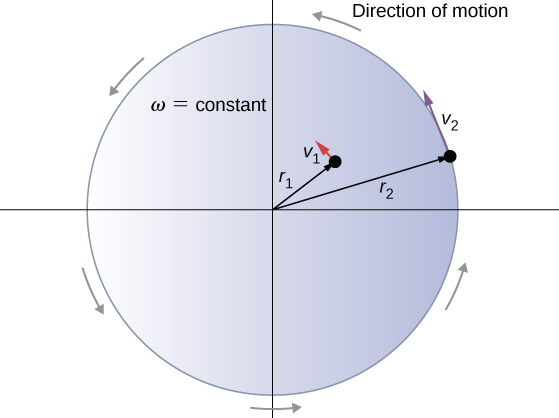
That is, the tangential speed of the particle is its angular velocity times the radius of the circle. From Equation 10.4, we see that the tangential speed of the particle increases with its distance from the axis of rotation for a constant angular velocity. This effect is shown in Figure 10.4. Two particles are placed at different radii on a rotating disk with a constant angular velocity. As the disk rotates, the tangential speed increases linearly with the radius from the axis of rotation. In Figure 10.4, we see that $v_1=r_1{\omega }_1$ and $v_2=r_2{\omega }_2$. But the disk has a constant angular velocity, so ${\omega }_1={\omega }_2$. This means $\frac{v_1}{r_1}=\frac{v_2}{r_2}$ or $v_2=\left(\frac{r_2}{r_1}\right)v_1$. Thus, since $r_2>r_1$, $v_2>v_1$.

Figure 10.4 Two particles on a rotating disk have different tangential speeds, depending on their distance to the axis of rotation.

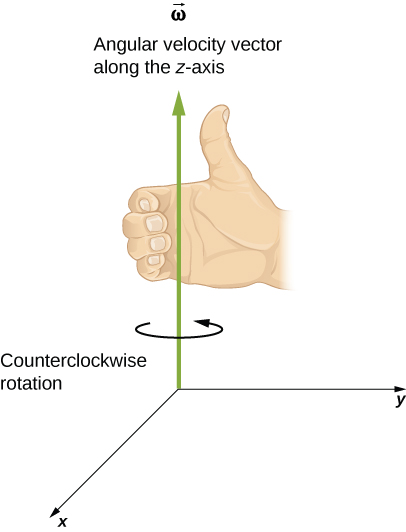
Up until now, we have discussed the magnitude of the angular velocity $\omega =d\theta \text{/}dt,$ which is a scalar quantity—the change in angular position with respect to time. The vector $\overrightarrow{\omega }$ is the vector associated with the angular velocity and points along the axis of rotation. This is useful because when a rigid body is rotating, we want to know both the axis of rotation and the direction that the body is rotating about the axis, clockwise or counterclockwise. The angular velocity $\overrightarrow{\omega }$ gives us this information. The angular velocity $\overrightarrow{\omega }$ has a direction determined by what is called the right-hand rule. The right-hand rule is such that if the fingers of your right hand wrap counterclockwise from the x-axis (the direction in which $\theta$ increases) toward the y-axis, your thumb points in the direction of the positive z-axis (Figure 10.5). An angular velocity $\overrightarrow{\omega }$ that points along the positive z-axis therefore corresponds to a counterclockwise rotation, whereas an angular velocity $\overrightarrow{\omega }$ that points along the negative z-axis corresponds to a clockwise rotation.

Figure 10.5 For counterclockwise rotation in the coordinate system shown, the angular velocity points in the positive z-direction by the right-hand-rule.

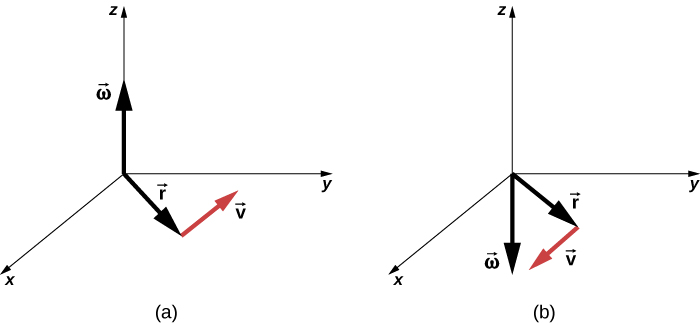
Similar to Equation 10.2, one can state a cross product relation to the vector of the tangential velocity as stated in Equation 10.4. Therefore, we have

That is, the tangential velocity is the cross product of the angular velocity and the position vector, as shown in Figure 10.6. From part (a) of this figure, we see that with the angular velocity in the positive z-direction, the rotation in the xy-plane is counterclockwise. In part (b), the angular velocity is in the negative z-direction, giving a clockwise rotation in the xy-plane.

Figure 10.6 The vectors shown are the angular velocity, position, and tangential velocity. (a) The angular velocity points in the positive z-direction, giving a counterclockwise rotation in the xy-plane. (b) The angular velocity points in the negative z-direction, giving a clockwise rotation.

Angular Acceleration

We have just discussed angular velocity for uniform circular motion, but not all motion is uniform. Envision an ice skater spinning with his arms outstretched—when he pulls his arms inward, his angular velocity increases. Or think about a computer’s hard disk slowing to a halt as the angular velocity decreases. We will explore these situations later, but we can already see a need to define an angular acceleration for describing situations where $\omega$ changes. The faster the change in $\omega$, the greater the angular acceleration. We define the instantaneous angular acceleration $\alpha$ as the derivative of angular velocity with respect to time:

where we have taken the limit of the average angular acceleration, $\bar{\alpha }=\frac{\text{Δ}\omega }{\text{Δ}t}$ as $\text{Δ}t\to 0$.

The units of angular acceleration are (rad/s)/s, or ${\text{rad/s}}^2$.

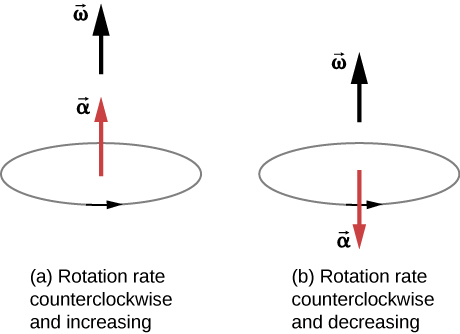
In the same way as we defined the vector associated with angular velocity $\overrightarrow{\omega }$, we can define $\overrightarrow{\alpha }$, the vector associated with angular acceleration (Figure 10.7). If the angular velocity is along the positive z-axis, as in Figure 10.5, and $\frac{d\omega }{dt}$ is positive, then the angular acceleration $\overrightarrow{\alpha }$ is positive and points along the $+z\text{-}$ axis. Similarly, if the angular velocity $\overrightarrow{\omega }$ is along the positive z-axis and $\frac{d\omega }{dt}$ is negative, then the angular acceleration is negative and points along the $–z-$ axis.

Figure 10.7 The rotation is counterclockwise in both (a) and (b) with the angular velocity in the same direction. (a) The angular acceleration is in the same direction as the angular velocity, which increases the rotation rate. (b) The angular acceleration is in the opposite direction to the angular velocity, which decreases the rotation rate.

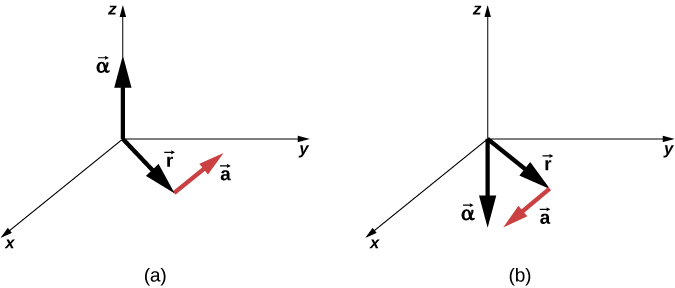
We can express the tangential acceleration vector as a cross product of the angular acceleration and the position vector. This expression can be found by taking the time derivative of $\overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{r}$ and is left as an exercise:

The vector relationships for the angular acceleration and tangential acceleration are shown in Figure 10.8.

Figure 10.8 (a) The angular acceleration is the positive z-direction and produces a tangential acceleration in a counterclockwise sense. (b) The angular acceleration is in the negative z-direction and produces a tangential acceleration in the clockwise sense.

We can relate the tangential acceleration of a point on a rotating body at a distance from the axis of rotation in the same way that we related the tangential speed to the angular velocity. If we differentiate Equation 10.4 with respect to time, noting that the radius r is constant, we obtain

Thus, the tangential acceleration $a_t$ is the radius times the angular acceleration. Equation 10.4 and Equation 10.8 are important for the discussion of rolling motion (see Angular Momentum).

Let’s apply these ideas to the analysis of a few simple fixed-axis rotation scenarios. Before doing so, we present a problem-solving strategy that can be applied to rotational kinematics: the description of rotational motion.

Now let’s apply this problem-solving strategy to a few specific examples.

Check Your Understanding 10.1

The fan blades on a turbofan jet engine (shown below) accelerate from rest up to a rotation rate of 40.0 rev/s in 20 s. The increase in angular velocity of the fan is constant in time. (The GE90-110B1 turbofan engine mounted on a Boeing 777, as shown, is currently the largest turbofan engine in the world, capable of thrusts of 330–510 kN.)

(a) What is the average angular acceleration?

(b) What is the instantaneous angular acceleration at any time during the first 20 s?

Figure 10.9 (credit: “Bubinator”/ Wikimedia Commons)

Example 10.3

Wind Turbine

A wind turbine (Figure 10.10) in a wind farm is being shut down for maintenance. It takes 30 s for the turbine to go from its operating angular velocity to a complete stop in which the angular velocity function is $\omega (t)=[{(t{\text{s}}^{\mathrm{-1}}\mathrm{-30.0})}^2\text{/}100.0]\text{rad}\text{/}\text{s}$, where $t$ is the time in seconds. If the turbine is rotating counterclockwise looking into the page, (a) what are the directions of the angular velocity and acceleration vectors? (b) What is the average angular acceleration? (c) What is the instantaneous angular acceleration at $t=0.0,15.0,30.0\text{s}?$

Figure 10.10 A wind turbine that is rotating counterclockwise, as seen head on.

Strategy

1. We are given the rotational sense of the turbine, which is counterclockwise in the plane of the page. Using the right hand rule (Figure 10.5), we can establish the directions of the angular velocity and acceleration vectors.
2. We calculate the initial and final angular velocities to get the average angular acceleration. We establish the sign of the angular acceleration from the results in (a).
3. We are given the functional form of the angular velocity, so we can find the functional form of the angular acceleration function by taking its derivative with respect to time.

Solution

1. Since the turbine is rotating counterclockwise, angular velocity $\overrightarrow{\omega }$ points out of the page. But since the angular velocity is decreasing, the angular acceleration $\overrightarrow{\alpha }$ points into the page, in the opposite sense to the angular velocity.
2. The initial angular velocity of the turbine, setting $t=0,\text{is}\omega =9.0\text{rad}\text{/}\text{s}$. The final angular velocity is zero, so the average angular acceleration is
   $$\bar{\alpha }=\frac{\text{Δ}\omega }{\text{Δ}t}=\frac{\omega -{\omega }_0}{t-t_0}=\frac{0-9.0\text{rad/s}}{30.0-0\text{s}}=\mathrm{-0.3}\text{rad}\text{/}{\text{s}}^2.$$
3. Taking the derivative of the angular velocity with respect to time gives $\alpha =\frac{d\omega }{dt}=(t-30.0)\text{/}50.0\text{rad}\text{/}{\text{s}}^2$
   $$\alpha (0.0\text{s})=\mathrm{-0.6}\text{rad}\text{/}{\text{s}}^2,\alpha (15.0\text{s})=\mathrm{-0.3}\text{rad}\text{/}{\text{s}}^2,\text{and}\alpha (30.0\text{s})=0\text{rad/s}.$$

Significance

We found from the calculations in (a) and (b) that the angular acceleration $\alpha$ and the average angular acceleration $\bar{\alpha }$ are negative. The turbine has an angular acceleration in the opposite sense to its angular velocity.

We now have a basic vocabulary for discussing fixed-axis rotational kinematics and relationships between rotational variables. We discuss more definitions and connections in the next section.