8.3 Conservation of Energy
Learning Objectives
By the end of this section, you will be able to:
- Formulate the principle of conservation of mechanical energy, with or without the presence of non-conservative forces
- Use the conservation of mechanical energy to calculate various properties of simple systems
In this section, we elaborate and extend the result we derived in Potential Energy of a System, where we re-wrote the work-energy theorem in terms of the change in the kinetic and potential energies of a particle. This will lead us to a discussion of the important principle of the conservation of mechanical energy. As you continue to examine other topics in physics, in later chapters of this book, you will see how this conservation law is generalized to encompass other types of energy and energy transfers. The last section of this chapter provides a preview.
The terms ‘conserved quantity’ and ‘conservation law’ have specific, scientific meanings in physics, which are different from the everyday meanings associated with the use of these words. (The same comment is also true about the scientific and everyday uses of the word ‘work.’) In everyday usage, you could conserve water by not using it, or by using less of it, or by re-using it. Water is composed of molecules consisting of two atoms of hydrogen and one of oxygen. Bring these atoms together to form a molecule and you create water; dissociate the atoms in such a molecule and you destroy water. However, in scientific usage, a conserved quantity for a system stays constant, changes by a definite amount that is transferred to other systems, and/or is converted into other forms of that quantity. A conserved quantity, in the scientific sense, can be transformed, but not strictly created or destroyed. Thus, there is no physical law of conservation of water.
Systems with a Single Particle or Object
We first consider a system with a single particle or object. Returning to our development of Equation 8.2, recall that we first separated all the forces acting on a particle into conservative and non-conservative types, and wrote the work done by each type of force as a separate term in the work-energy theorem. We then replaced the work done by the conservative forces by the change in the potential energy of the particle, combining it with the change in the particle’s kinetic energy to get Equation 8.2. Now, we write this equation without the middle step and define the sum of the kinetic and potential energies, to be the mechanical energy of the particle.
Conservation of Energy
The mechanical energy E of a particle stays constant unless forces outside the system or non-conservative forces do work on it, in which case, the change in the mechanical energy is equal to the work done by the non-conservative forces:
This statement expresses the concept of energy conservation for a classical particle as long as there is no non-conservative work. Recall that a classical particle is just a point mass, is nonrelativistic, and obeys Newton’s laws of motion. In Relativity, we will see that conservation of energy still applies to a non-classical particle, but for that to happen, we have to make a slight adjustment to the definition of energy.
It is sometimes convenient to separate the case where the work done by non-conservative forces is zero, either because no such forces are assumed present, or, like the normal force, they do zero work when the motion is parallel to the surface. Then
In this case, the conservation of mechanical energy can be expressed as follows: The mechanical energy of a particle does not change if all the non-conservative forces that may act on it do no work. Understanding the concept of energy conservation is the important thing, not the particular equation you use to express it.
Problem-Solving Strategy
Conservation of Energy
- Identify the body or bodies to be studied (the system). Often, in applications of the principle of mechanical energy conservation, we study more than one body at the same time.
- Identify all forces acting on the body or bodies.
- Determine whether each force that does work is conservative. If a non-conservative force (e.g., friction) is doing work, then mechanical energy is not conserved. The system must then be analyzed with non-conservative work, Equation 8.12.
- For every conservative force that does work, choose a reference point and determine the potential energy function for the force. The reference points for the various potential energies do not have to be at the same location.
- If no non-conservative work is done, apply the principle of mechanical energy conservation by setting the sum of the kinetic energies and potential energies equal at every point of interest.
Example 8.7
Simple Pendulum
A particle of mass m is hung from the ceiling by a massless string of length 1.0 m, as shown in Figure 8.7. The particle is released from rest, when the angle between the string and the downward vertical direction is What is its speed when it reaches the lowest point of its arc?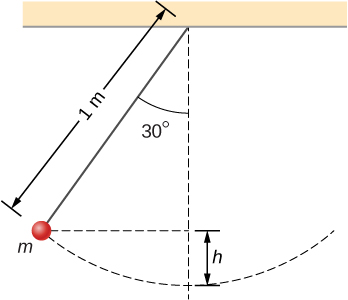
Strategy
Using our problem-solving strategy, the first step is to define that we are interested in the particle-Earth system. Second, only the gravitational force is acting on the particle, which is conservative (step 3). We neglect air resistance in the problem, and no work is done by the string tension, which is perpendicular to the arc of the motion. Therefore, the mechanical energy of the system is conserved, as represented by Equation 8.13, . Because the particle starts from rest, the increase in the kinetic energy is just the kinetic energy at the lowest point. This increase in kinetic energy equals the decrease in the gravitational potential energy, which we can calculate from the geometry. In step 4, we choose a reference point for zero gravitational potential energy to be at the lowest vertical point the particle achieves, which is mid-swing. Lastly, in step 5, we set the sum of energies at the highest point (initial) of the swing to the lowest point (final) of the swing to ultimately solve for the final speed.Solution
We are neglecting non-conservative forces, so we write the energy conservation formula relating the particle at the highest point (initial) and the lowest point in the swing (final) asSince the particle is released from rest, the initial kinetic energy is zero. At the lowest point, we define the gravitational potential energy to be zero. Therefore our conservation of energy formula reduces to
The vertical height of the particle is not given directly in the problem. This can be solved for by using trigonometry and two givens: the length of the pendulum and the angle through which the particle is vertically pulled up. Looking at the diagram, the vertical dashed line is the length of the pendulum string. The vertical height is labeled h. The other partial length of the vertical string can be calculated with trigonometry. That piece is solved for by
Therefore, by looking at the two parts of the string, we can solve for the height h,
We substitute this height into the previous expression solved for speed to calculate our result:
Significance
We found the speed directly from the conservation of mechanical energy, without having to solve the differential equation for the motion of a pendulum (see Oscillations). We can approach this problem in terms of bar graphs of total energy. Initially, the particle has all potential energy, being at the highest point, and no kinetic energy. When the particle crosses the lowest point at the bottom of the swing, the energy moves from the potential energy column to the kinetic energy column. Therefore, we can imagine a progression of this transfer as the particle moves between its highest point, lowest point of the swing, and back to the highest point (Figure 8.8). As the particle travels from the lowest point in the swing to the highest point on the far right hand side of the diagram, the energy bars go in reverse order from (c) to (b) to (a).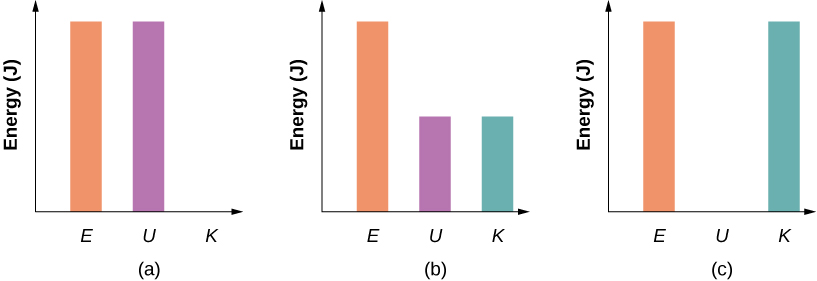
Check Your Understanding 8.7
How high above the bottom of its arc is the particle in the simple pendulum above, when its speed is
Example 8.8
Air Resistance on a Falling Object
A helicopter is hovering at an altitude of when a panel from its underside breaks loose and plummets to the ground (Figure 8.9). The mass of the panel is and it hits the ground with a speed of . How much mechanical energy was dissipated by air resistance during the panel’s descent?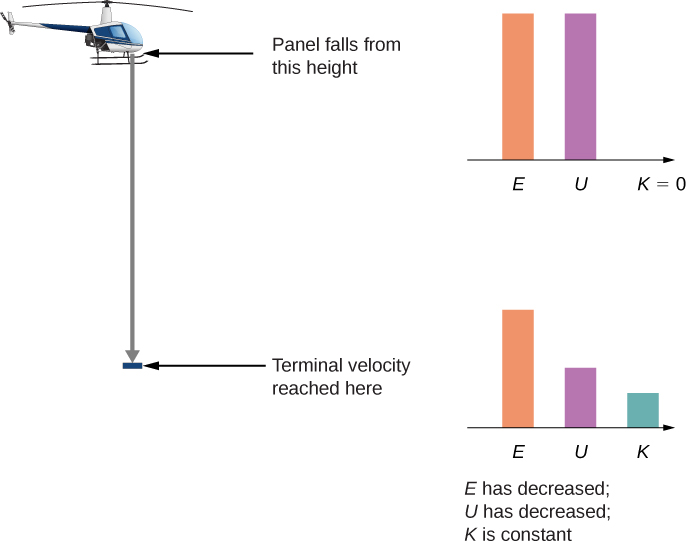
Strategy
Step 1: Here only one body is being investigated.Step 2: Gravitational force is acting on the panel, as well as air resistance, which is stated in the problem.
Step 3: Gravitational force is conservative; however, the non-conservative force of air resistance does negative work on the falling panel, so we can use the conservation of mechanical energy, in the form expressed by Equation 8.12, to find the energy dissipated. This energy is the magnitude of the work:
Step 4: The initial kinetic energy, at is zero. We set the gravitational potential energy to zero at ground level out of convenience.
Step 5: The non-conservative work is set equal to the energies to solve for the work dissipated by air resistance.
Solution
The mechanical energy dissipated by air resistance is the algebraic sum of the gain in the kinetic energy and loss in potential energy. Therefore the calculation of this energy isSignificance
Most of the initial mechanical energy of the panel , 147 kJ, was lost to air resistance. Notice that we were able to calculate the energy dissipated without knowing what the force of air resistance was, only that it was dissipative.Check Your Understanding 8.8
You probably recall that, neglecting air resistance, if you throw a projectile straight up, the time it takes to reach its maximum height equals the time it takes to fall from the maximum height back to the starting height. Suppose you cannot neglect air resistance, as in Example 8.8. Is the time the projectile takes to go up (a) greater than, (b) less than, or (c) equal to the time it takes to come back down? Explain.
In these examples, we were able to use conservation of energy to calculate the speed of a particle just at particular points in its motion. But the method of analyzing particle motion, starting from energy conservation, is more powerful than that. More advanced treatments of the theory of mechanics allow you to calculate the full time dependence of a particle’s motion, for a given potential energy. In fact, it is often the case that a better model for particle motion is provided by the form of its kinetic and potential energies, rather than an equation for force acting on it. (This is especially true for the quantum mechanical description of particles like electrons or atoms.)
We can illustrate some of the simplest features of this energy-based approach by considering a particle in one-dimensional motion, with potential energy U(x) and no non-conservative interactions present. Equation 8.12 and the definition of velocity require
Separate the variables x and t and integrate, from an initial time to an arbitrary time, to get
If you can do the integral in Equation 8.14, then you can solve for x as a function of t.
Example 8.9
Constant Acceleration
Use the potential energy for in Equation 8.14 to find the position x of a particle as a function of time t.Strategy
Since we know how the potential energy changes as a function of x, we can substitute for in Equation 8.14, integrate, and then solve for x. This results in an expression of x as a function of time with constants of energy E, mass m, and the initial positionSolution
Following the first two suggested steps in the above strategy,Solving for the position, we obtain .
Significance
The position as a function of time, for this potential, represents one-dimensional motion with constant acceleration, starting at rest from position This is not so surprising, since this is a potential energy for a constant force, andCheck Your Understanding 8.9
What potential energy can you substitute in Equation 8.13 that will result in motion with constant velocity of 2 m/s for a particle of mass 1 kg and mechanical energy 1 J?
We will look at another more physically appropriate example of the use of Equation 8.13 after we have explored some further implications that can be drawn from the functional form of a particle’s potential energy.
Systems with Several Particles or Objects
Systems generally consist of more than one particle or object. However, the conservation of mechanical energy, in one of the forms in Equation 8.12 or Equation 8.13, is a fundamental law of physics and applies to any system. You just have to include the kinetic and potential energies of all the particles, and the work done by all the non-conservative forces acting on them. Until you learn more about the dynamics of systems composed of many particles, in Linear Momentum and Collisions, Fixed-Axis Rotation, and Angular Momentum, it is better to postpone discussing the application of energy conservation to then.