Challenge Problems

88.

Vector $\vec{B}$ is 5.0 cm long and vector $\vec{A}$ is 4.0 cm long. Find the angle between these two vectors when $| \vec{A} + \vec{B} | = 3.0 cm$ .

89.

What is the component of the force vector $\vec{G} = (3.0 \hat{i} + 4.0 \hat{j} + 10.0 \hat{k}) N$ along the force vector $\vec{H} = (1.0 \hat{i} + 4.0 \hat{j}) N$ ?

90.

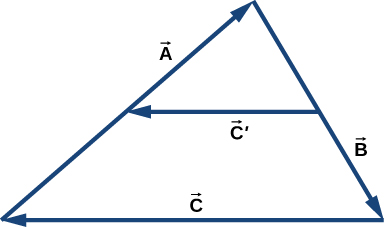
The following figure shows a triangle formed by the three vectors $\vec{A}$ , $\vec{B}$ , and $\vec{C}$ . If vector ${\vec{C}}^{'}$ is drawn between the midpoints of vectors $\vec{A}$ and $\vec{B}$ , show that ${\vec{C}}^{'} = \vec{C} / 2$ .

Vectors A, B and C form a triangle. Vector A points up and right, vector B starts at the head of A and points down and right, and vector C starts at the head of B, ends at the tail of A and points to the left. Vector C prime is parallel to vector C and connects the midpoints of vectors A and B.

91.

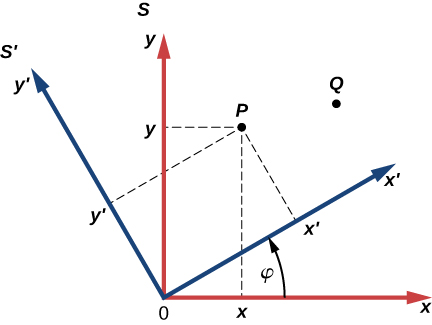
Distances between points in a plane do not change when a coordinate system is rotated. In other words, the magnitude of a vector is invariant under rotations of the coordinate system. Suppose a coordinate system S is rotated about its origin by angle $φ$ to become a new coordinate system $S^{'}$ , as shown in the following figure. A point in a plane has coordinates (x, y) in S and coordinates $(x^{'}, y^{'})$ in $S^{'}$ .

(a) Show that, during the transformation of rotation, the coordinates in $S^{'}$ are expressed in terms of the coordinates in S by the following relations:

{\begin{matrix} x^{'} = x cos φ + y sin φ \\ y^{'} = − x sin φ + y cos φ \end{matrix} .

(b) Show that the distance of point P to the origin is invariant under rotations of the coordinate system. Here, you have to show that

\sqrt{x^{2} + y^{2}} = \sqrt{{x^{'}}^{2} + {y^{'}}^{2}} .

(c) Show that the distance between points P and Q is invariant under rotations of the coordinate system. Here, you have to show that

\sqrt{{(x_{P} - x_{Q})}^{2} + {(y_{P} - y_{Q})}^{2}} = \sqrt{{({x^{'}}_{P} - {x^{'}}_{Q})}^{2} + {({y^{'}}_{P} - {y^{'}}_{Q})}^{2}} .

Two coordinate systems are shown. The x y coordinate system S, in red, has positive x to to the right and positive y up. The x prime y prime coordinate system S prime, in blue, shares the same origin as S but is rotated relative to S counterclockwise an angle phi. Two points, P and Q are shown. Point P’s x coordinate in frame S is shown as a dashed line from P to the x axis, drawn parallel to the y axis. Point P’s y coordinate in frame S is shown as a dashed line from P to the y axis, drawn parallel to the x axis. Point P’s x prime coordinate in frame S prime is shown as a dashed line from P to the x prime axis, drawn parallel to the y prime axis. Point P’s y prime coordinate in frame S prime is shown as a dashed line from P to the y prime axis, drawn parallel to the x prime axis.