9.7 Rocket Propulsion

Learning Objectives

By the end of this section, you will be able to:

Describe the application of conservation of momentum when the mass changes with time, as well as the velocity
Calculate the speed of a rocket in empty space, at some time, given initial conditions
Calculate the speed of a rocket in Earth’s gravity field, at some time, given initial conditions

Now we deal with the case where the mass of an object is changing. We analyze the motion of a rocket, which changes its velocity (and hence its momentum) by ejecting burned fuel gases, thus causing it to accelerate in the opposite direction of the velocity of the ejected fuel (see Figure 9.32). Specifically: A fully fueled rocket ship in deep space has a total mass $m_{0}$ (this mass includes the initial mass of the fuel). At some moment in time, the rocket has a velocity $\vec{v}$ and mass m; this mass is a combination of the mass of the empty rocket and the mass of the remaining unburned fuel it contains. (We refer to m as the “instantaneous mass” and $\vec{v}$ as the “instantaneous velocity.”) The rocket accelerates by burning the fuel it carries and ejecting the burned exhaust gases. If the burn rate of the fuel is constant, and the velocity at which the exhaust is ejected is also constant, what is the change of velocity of the rocket as a result of burning all of its fuel?

A photograph of the space shuttle taking off.

Figure 9.32 The space shuttle had a number of reusable parts. Solid fuel boosters on either side were recovered and refueled after each flight, and the entire orbiter returned to Earth for use in subsequent flights. The large liquid fuel tank was expended. The space shuttle was a complex assemblage of technologies, employing both solid and liquid fuel, and pioneering ceramic tiles as reentry heat shields. As a result, it permitted multiple launches as opposed to single-use rockets. (credit: modification of work by NASA)

Physical Analysis

Here’s a description of what happens, so that you get a feel for the physics involved.

As the rocket engines operate, they are continuously ejecting burned fuel gases, which have both mass and velocity, and therefore some momentum. By conservation of momentum, the rocket’s momentum changes by this same amount (with the opposite sign). We will assume the burned fuel is being ejected at a constant rate, which means the rate of change of the rocket’s momentum is also constant. By Equation 9.9, this represents a constant force on the rocket.
However, as time goes on, the mass of the rocket (which includes the mass of the remaining fuel) continuously decreases. Thus, even though the force on the rocket is constant, the resulting acceleration is not; it is continuously increasing.
So, the total change of the rocket’s velocity will depend on the amount of mass of fuel that is burned, and that dependence is not linear.

The problem has the mass and velocity of the rocket changing; also, the total mass of ejected gases is changing. If we define our system to be the rocket + fuel, then this is a closed system (since the rocket is in deep space, there are no external forces acting on this system); as a result, momentum is conserved for this system. Thus, we can apply conservation of momentum to answer the question (Figure 9.33).

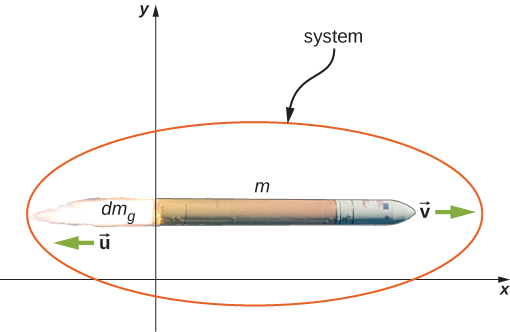
An x y coordinate system is shown. A rocket mass m is moving to the right with velocity v. the rocket’s exhaust mass d m sub g is moving to the left with velocity u. The system consists of the rocket and the exhaust.

Figure 9.33 The rocket accelerates to the right due to the expulsion of some of its fuel mass to the left. Conservation of momentum enables us to determine the resulting change of velocity. The mass m is the instantaneous total mass of the rocket (i.e., mass of rocket body plus mass of fuel at that point in time). (credit: modification of work by NASA/Bill Ingalls)

At the same moment that the total instantaneous rocket mass is m (i.e., m is the mass of the rocket body plus the mass of the fuel at that point in time), we define the rocket’s instantaneous velocity to be $\vec{v} = v \hat{i}$ (in the +x-direction); this velocity is measured relative to an inertial reference system (the Earth, for example). Thus, the initial momentum of the system is

${\vec{p}}_{i} = m v \hat{i} .$

The rocket’s engines are burning fuel at a constant rate and ejecting the exhaust gases in the −x-direction. During an infinitesimal time interval dt, the engines eject a (positive) infinitesimal mass of gas $d m_{g}$ at velocity $\vec{u} = − u \hat{i}$ ; note that although the rocket velocity $v \hat{i}$ is measured with respect to Earth, the exhaust gas velocity is measured with respect to the (moving) rocket. Measured with respect to the Earth, therefore, the exhaust gas has velocity $(v - u) \hat{i}$ .

As a consequence of the ejection of the fuel gas, the rocket’s mass decreases by $d m_{g}$ , and its velocity increases by $d v \hat{i}$ . Therefore, including both the change for the rocket and the change for the exhaust gas, the final momentum of the system is

\begin{matrix} {\vec{p}}_{f} & = {\vec{p}}_{rocket} + {\vec{p}}_{gas} \\ = (m - d m_{g}) (v + d v) \hat{i} + d m_{g} (v - u) \hat{i} \end{matrix} .

Since all vectors are in the x-direction, we drop the vector notation. Applying conservation of momentum, we obtain

\begin{array}{l} p_{i} = p_{f} \\ m v = (m - d m_{g}) (v + d v) + d m_{g} (v - u) \\ m v = m v + m d v - d m_{g} v - d m_{g} d v + d m_{g} v - d m_{g} u \\ m d v = d m_{g} d v + d m_{g} u . \end{array}

Now, $d m_{g}$ and dv are each very small; thus, their product $d m_{g} d v$ is very, very small, much smaller than the other two terms in this expression. We neglect this term, therefore, and obtain:

m d v = d m_{g} u .

Our next step is to remember that, since $d m_{g}$ represents an increase in the mass of ejected gases, it must also represent a decrease of mass of the rocket:

d m_{g} = − d m .

Replacing this, we have

m d v = − d m u

d v = − u \frac{d m}{m} .

Integrating from the initial mass m₀ to the final mass m of the rocket gives us the result we are after:

\begin{matrix} \int_{v_{i}}^{v} d v & = & − u \int_{m_{0}}^{m} \frac{1}{m} d m \\ v - v_{i} & = & u ln (\frac{m_{0}}{m}) \end{matrix}

and thus our final answer is

Δ v = u ln (\frac{m_{0}}{m}) .

9.38

This result is called the rocket equation. It was originally derived by the Russian rocket scientist Konstantin Tsiolkovsky in 1897. It gives us the change of velocity that the rocket obtains from burning a mass of fuel that decreases the total rocket mass from $m_{0}$ down to m. As expected, the relationship between $Δ v$ and the change of mass of the rocket is nonlinear.

Problem-Solving Strategy

Rocket Propulsion

In rocket problems, the most common questions are finding the change of velocity due to burning some amount of fuel for some amount of time; or to determine the acceleration that results from burning fuel.

To determine the change of velocity, use the rocket equation Equation 9.38.
To determine the acceleration, determine the force by using the impulse-momentum theorem, using the rocket equation to determine the change of velocity.

Example 9.20

Thrust on a Spacecraft

A spacecraft is moving in gravity-free space along a straight path when its pilot decides to accelerate forward. He turns on the thrusters, and burned fuel is ejected at a constant rate of

2.0 \times 10^{2} kg/s

, at a speed (relative to the rocket) of

2.5 \times 10^{2} m/s

. The initial mass of the spacecraft and its unburned fuel is

2.0 \times 10^{4} kg

, and the thrusters are on for 30 s.

What is the thrust (the force applied to the rocket by the ejected fuel) on the spacecraft?
What is the spacecraft’s acceleration as a function of time?
What are the spacecraft’s accelerations at t = 0, 15, 30, and 35 s?

Strategy

The force on the spacecraft is equal to the rate of change of the momentum of the fuel.
Knowing the force from part (a), we can use Newton’s second law to calculate the consequent acceleration. The key here is that, although the force applied to the spacecraft is constant (the fuel is being ejected at a constant rate), the mass of the spacecraft isn’t; thus, the acceleration caused by the force won’t be constant. We expect to get a function a(t), therefore.
We’ll use the function we obtain in part (b), and just substitute the numbers given. Important: We expect that the acceleration will get larger as time goes on, since the mass being accelerated is continuously decreasing (fuel is being ejected from the rocket).

Solution

The momentum of the ejected fuel gas is
$p = m_{g} v .$
The ejection velocity $v = 2.5 \times 10^{2} m/s$ is constant, and therefore the force is
$F = \frac{d p}{d t} = v \frac{d m_{g}}{d t} = − v \frac{d m}{d t} .$
Now, $\frac{d m_{g}}{d t}$ is the rate of change of the mass of the fuel; the problem states that this is $2.0 \times 10^{2} kg/s$ . Substituting, we get
$\begin{matrix} F & = v \frac{d m_{g}}{d t} \\ = (2.5 \times 10^{2} \frac{m}{s}) (2.0 \times 10^{2} \frac{kg}{s}) \\ = 5 \times 10^{4} N. \end{matrix}$
Above, we defined m to be the combined mass of the empty rocket plus however much unburned fuel it contained: $m = m_{R} + m_{g}$ . From Newton’s second law,
$a = \frac{F}{m} = \frac{F}{m_{R} + m_{g}} .$
The force is constant and the empty rocket mass $m_{R}$ is constant, but the fuel mass $m_{g}$ is decreasing at a uniform rate; specifically:
$m_{g} = m_{g} (t) = m_{g_{0}} - (\frac{d m_{g}}{d t}) t .$
This gives us
$a (t) = \frac{F}{m_{g_{i}} - (\frac{d m_{g}}{d t}) t} = \frac{F}{M - (\frac{d m_{g}}{d t}) t} .$
Notice that, as expected, the acceleration is a function of time. Substituting the given numbers:
$a (t) = \frac{5 \times 10^{4} N}{2.0 \times 10^{4} kg - (2.0 \times 10^{2} \frac{kg}{s}) t} .$
At $t = 0 s$ :
$a (0 s) = \frac{5 \times 10^{4} N}{2.0 \times 10^{4} kg - (2.0 \times 10^{2} \frac{kg}{s}) (0 s)} = 2.5 \frac{m}{s^{2}} .$
At $t = 15 s, a (15 s) = {2.9 m/s}^{2}$ .
At $t = 30 s, a (30 s) = 3.6 {m/s}^{2}$ .
Acceleration is increasing, as we expected.
At $t = 35 s$ (and at any time after $t = 30 s$ ), the acceleration is $0 {m/s}^{2}$ since the thrusters stopped working and thus no external forces are acting on the spacecraft.

Significance

Notice that the acceleration is not constant; as a result, any dynamical quantities must be calculated either using integrals, or (more easily) conservation of total energy.

Check Your Understanding 9.14

What is the physical difference (or relationship) between $\frac{d m}{d t}$ and $\frac{d m_{g}}{d t}$ in this example?

Rocket in a Gravitational Field

Let’s now analyze the velocity change of the rocket during the launch phase, from the surface of Earth. To keep the math manageable, we’ll restrict our attention to distances for which the acceleration caused by gravity can be treated as a constant g.

The analysis is similar, except that now there is an external force of $\vec{F} = − m g \hat{j}$ acting on our system. This force applies an impulse $d \vec{J} = \vec{F} d t = − m g d t \hat{j}$ , which is equal to the change of momentum. This gives us

\begin{matrix} d \vec{p} & = & d \vec{J} \\ {\vec{p}}_{f} - {\vec{p}}_{i} & = & − m g d t \hat{j} \\ [(m - d m_{g}) (v + d v) + d m_{g} (v - u) - m v] \hat{j} & = & − m g d t \hat{j} \end{matrix}

and so

m d v - d m_{g} u = − m g d t

where we have again neglected the term $d m_{g} d v$ and dropped the vector notation. Next we replace $d m_{g}$ with $− d m$ :

\begin{matrix} m d v + d m u & = & − m g d t \\ m d v & = & − d m u - m g d t . \end{matrix}

Dividing through by m gives

d v = − u \frac{d m}{m} - g d t

and integrating, we have

Δ v = u ln (\frac{m_{0}}{m}) - g Δ t .

9.39

Unsurprisingly, the rocket’s velocity is affected by the (constant) acceleration of gravity.

Remember that $Δ t$ is the burn time of the fuel. Now, in the absence of gravity, Equation 9.38 implies that it makes no difference how much time it takes to burn the entire mass of fuel; the change of velocity does not depend on $Δ t$ . However, in the presence of gravity, it matters a lot. The −g $Δ t$ term in Equation 9.39 tells us that the longer the burn time is, the smaller the rocket’s change of velocity will be. This is the reason that the launch of a rocket is so spectacular at the first moment of liftoff: It’s essential to burn the fuel as quickly as possible, to get as large a $Δ v$ as possible.