9.2 Impulse and Collisions
Learning Objectives
By the end of this section, you will be able to:
- Explain what an impulse is, physically
- Describe what an impulse does
- Relate impulses to collisions
- Apply the impulse-momentum theorem to solve problems
We have defined momentum to be the product of mass and velocity. Therefore, if an object’s velocity should change (due to the application of a force on the object), then necessarily, its momentum changes as well. This indicates a connection between momentum and force. The purpose of this section is to explore and describe that connection.
Suppose you apply a force on a free object for some amount of time. Clearly, the larger the force, the larger the object’s change of momentum will be. Alternatively, the more time you spend applying this force, again the larger the change of momentum will be, as depicted in Figure 9.5. The amount by which the object’s motion changes is therefore proportional to the magnitude of the force, and also to the time interval over which the force is applied.
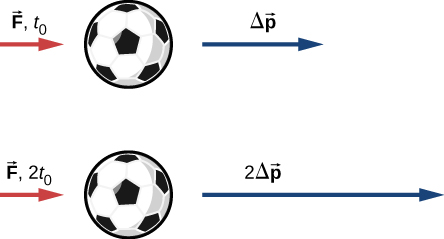
Mathematically, if a quantity is proportional to two (or more) things, then it is proportional to the product of those things. The product of a force and a time interval (over which that force acts) is called impulse, and is given the symbol
Impulse
Let be the force applied to an object over some differential time interval dt (Figure 9.6). The resulting impulse on the object is defined as
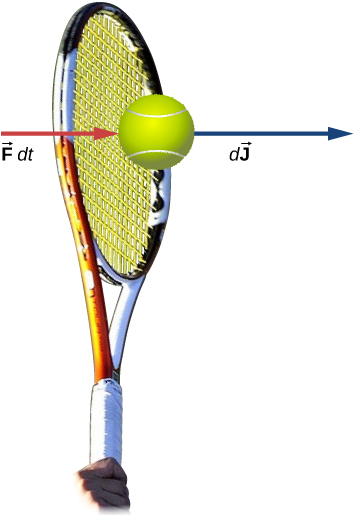
The total impulse over the interval is
Equation 9.2 and Equation 9.3 together say that when a force is applied for an infinitesimal time interval dt, it causes an infinitesimal impulse , and the total impulse given to the object is defined to be the sum (integral) of all these infinitesimal impulses.
To calculate the impulse using Equation 9.3, we need to know the force function F(t), which we often don’t. However, a result from calculus is useful here: Recall that the average value of a function over some interval is calculated by
where . Applying this to the time-dependent force function, we obtain
Therefore, from Equation 9.3,
The idea here is that you can calculate the impulse on the object even if you don’t know the details of the force as a function of time; you only need the average force. In fact, though, the process is usually reversed: You determine the impulse (by measurement or calculation) and then calculate the average force that caused that impulse.
To calculate the impulse, a useful result follows from writing the force in Equation 9.3 as :
For a constant force , this simplifies to
That is,
Note that the integral form, Equation 9.3, applies to constant forces as well; in that case, since the force is independent of time, it comes out of the integral, which can then be trivially evaluated.
Example 9.1
The Arizona Meteor Crater
Approximately 50,000 years ago, a large (radius of 25 m) iron-nickel meteorite collided with Earth at an estimated speed of in what is now the northern Arizona desert, in the United States. The impact produced a crater that is still visible today (Figure 9.7); it is approximately 1200 m (three-quarters of a mile) in diameter, 170 m deep, and has a rim that rises 45 m above the surrounding desert plain. Iron-nickel meteorites typically have a density of . Use impulse considerations to estimate the average force and the maximum force that the meteor applied to Earth during the impact.
Strategy
It is conceptually easier to reverse the question and calculate the force that Earth applied on the meteor in order to stop it. Therefore, we’ll calculate the force on the meteor and then use Newton’s third law to argue that the force from the meteor on Earth was equal in magnitude and opposite in direction.Using the given data about the meteor, and making reasonable guesses about the shape of the meteor and impact time, we first calculate the impulse using Equation 9.6. We then use the relationship between force and impulse Equation 9.5 to estimate the average force during impact. Next, we choose a reasonable force function for the impact event, calculate the average value of that function Equation 9.4, and set the resulting expression equal to the calculated average force. This enables us to solve for the maximum force.
Solution
Define upward to be the +y-direction. For simplicity, assume the meteor is traveling vertically downward prior to impact. In that case, its initial velocity is , and the force Earth exerts on the meteor points upward, . The situation at is depicted below.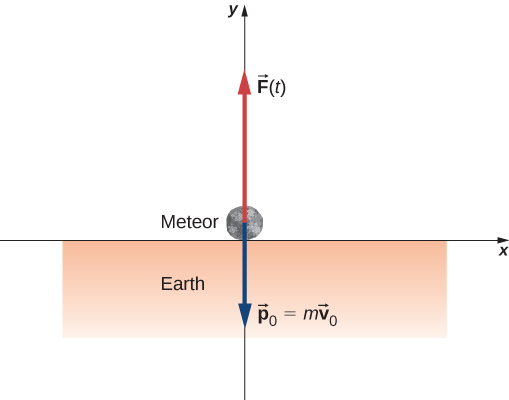
The average force during the impact is related to the impulse by
From Equation 9.6, , so we have
The mass is equal to the product of the meteor’s density and its volume:
If we assume (guess) that the meteor was roughly spherical, we have
Thus we obtain
The problem says the velocity at impact was (the final velocity is zero); also, we guess that the primary impact lasted about . Substituting these values gives
This is the average force applied during the collision. Notice that this force vector points in the same direction as the change of velocity vector .
Next, we calculate the maximum force. The impulse is related to the force function by
We need to make a reasonable choice for the force as a function of time. We define to be the moment the meteor first touches the ground. Then we assume the force is a maximum at impact, and rapidly drops to zero. A function that does this is
(The parameter represents how rapidly the force decreases to zero.) The average force is
where . Since we already have a numeric value for , we can use the result of the integral to obtain .
Choosing (this is a common choice, as you will see in later chapters), and guessing that , this integral evaluates to
Thus, the maximum force has a magnitude of
The complete force function, including the direction, is
This is the force Earth applied to the meteor; by Newton’s third law, the force the meteor applied to Earth is
which is the answer to the original question.
Significance
The graph of this function contains important information. Let’s graph (the magnitude of) both this function and the average force together (Figure 9.8).
Notice that the area under each plot has been filled in. For the plot of the (constant) force , the area is a rectangle, corresponding to . As for the plot of F(t), recall from calculus that the area under the plot of a function is numerically equal to the integral of that function, over the specified interval; so here, that is . Thus, the areas are equal, and both represent the impulse that the meteor applied to Earth during the two-second impact. The average force on Earth sounds like a huge force, and it is. Nevertheless, Earth barely noticed it. The acceleration Earth obtained was just
which is completely immeasurable. That said, the impact created seismic waves that nowadays could be detected by modern monitoring equipment.
Example 9.2
The Benefits of Impulse
A car traveling at 27 m/s collides with a building. The collision with the building causes the car to come to a stop in approximately 1 second. The driver, who weighs 860 N, is protected by a combination of a variable-tension seatbelt and an airbag (Figure 9.9). (In effect, the driver collides with the seatbelt and airbag and not with the building.) The airbag and seatbelt slow his velocity, such that he comes to a stop in approximately 2.5 s.- What average force does the driver experience during the collision?
- Without the seatbelt and airbag, his collision time (with the steering wheel) would have been approximately 0.20 s. What force would he experience in this case?
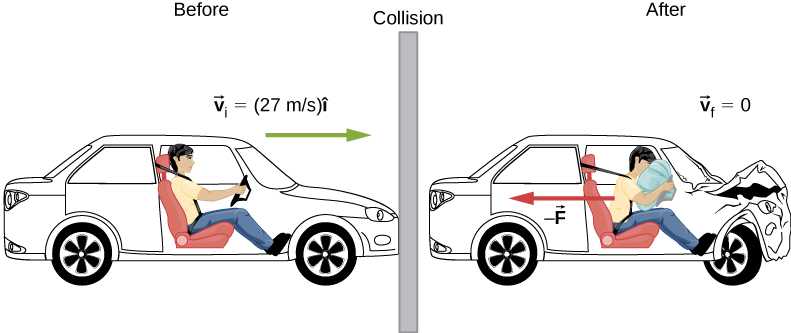
Strategy
We are given the driver’s weight, his initial and final velocities, and the time of collision; we are asked to calculate a force. Impulse seems the right way to tackle this; we can combine Equation 9.5 and Equation 9.6.Solution
- Define the +x-direction to be the direction the car is initially moving. We know and Since J is equal to both those things, they must be equal to each other: We need to convert this weight to the equivalent mass, expressed in SI units: Remembering that , and noting that the final velocity is zero, we solve for the force: The negative sign implies that the force slows him down. For perspective, this is about 1.1 times his own weight.
- Same calculation, just the different time interval: which is about 14 times his own weight. Big difference!
Significance
You see that the value of an airbag is how greatly it reduces the force on the vehicle occupants. For this reason, they have been required on all passenger vehicles in the United States since 1991, and have been commonplace throughout Europe and Asia since the mid-1990s. The change of momentum in a crash is the same, with or without an airbag; the force, however, is vastly different.Effect of Impulse
Since an impulse is a force acting for some amount of time, it causes an object’s motion to change. Recall Equation 9.6:
Because is the momentum of a system, is the change of momentum . This gives us the following relation, called the impulse-momentum theorem (or relation).
Impulse-Momentum Theorem
An impulse applied to a system changes the system’s momentum, and that change of momentum is exactly equal to the impulse that was applied:
The impulse-momentum theorem is depicted graphically in Figure 9.10.
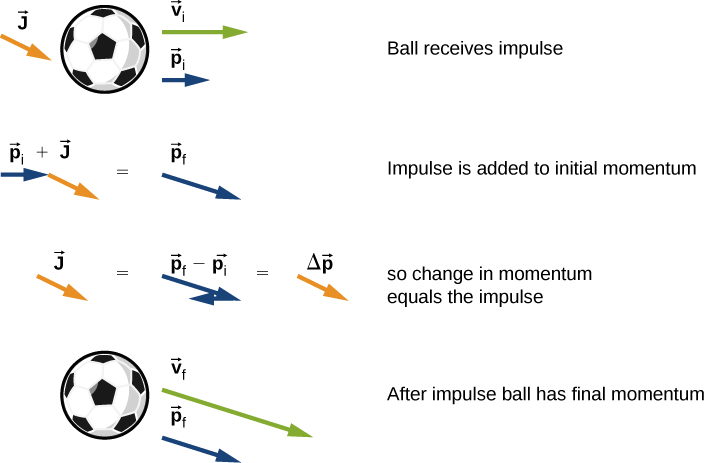
There are two crucial concepts in the impulse-momentum theorem:
- Impulse is a vector quantity; an impulse of, say, is very different from an impulse of ; they cause completely opposite changes of momentum.
- An impulse does not cause momentum; rather, it causes a change in the momentum of an object. Thus, you must subtract the initial momentum from the final momentum, and—since momentum is also a vector quantity—you must take careful account of the signs of the momentum vectors.
The most common questions asked in relation to impulse are to calculate the applied force, or the change of velocity that occurs as a result of applying an impulse. The general approach is the same.
Problem-Solving Strategy
Impulse-Momentum Theorem
- Express the impulse as force times the relevant time interval.
- Express the impulse as the change of momentum, usually .
- Equate these and solve for the desired quantity.
Example 9.3
Moving the Enterprise

When Captain Picard commands, “Take us out,” the starship Enterprise (Figure 9.11) starts from rest to a final speed of . Assuming this maneuver is completed in 60 s, what average force did the impulse engines apply to the ship?
Strategy
We are asked for a force; we know the initial and final speeds (and hence the change in speed), and we know the time interval over which this all happened. In particular, we know the amount of time that the force acted. This suggests using the impulse-momentum relation. To use that, though, we need the mass of the Enterprise. An internet search gives a best estimate of the mass of the Enterprise (in the 2009 movie) as .Solution
Because this problem involves only one direction (i.e., the direction of the force applied by the engines), we only need the scalar form of the impulse-momentum theorem Equation 9.7, which iswith
and
Equating these expressions gives
Solving for the magnitude of the force and inserting the given values leads to
Significance
Using Newton's Second Law, this force causes an acceleration of . This is 130,000 times gravity, which is unimaginably huge. It goes almost without saying that such a force would kill everyone on board instantly, as well as destroying every piece of equipment. Fortunately, the Enterprise has “inertial dampeners.” It is left as an exercise for the reader’s imagination to determine how these work.Check Your Understanding 9.1
The U.S. Air Force uses “10gs” (an acceleration equal to ) as the maximum acceleration a human can withstand (but only for several seconds) and survive. How much time must the Enterprise spend accelerating if the humans on board are to experience an average of at most 10gs of acceleration? (Assume the inertial dampeners are offline.)
Example 9.4
The iPhone Drop
Apple released its iPhone 6 Plus in November 2014. According to many reports, it was originally supposed to have a screen made from sapphire, but that was changed at the last minute for a hardened glass screen. Reportedly, this was because the sapphire screen cracked when the phone was dropped. What force did the iPhone 6 Plus experience as a result of being dropped?Strategy
The force the phone experiences is due to the impulse applied to it by the floor when the phone collides with the floor. Our strategy then is to use the impulse-momentum relationship. We calculate the impulse, estimate the impact time, and use this to calculate the force.We need to make a couple of reasonable estimates, as well as find technical data on the phone itself. First, let’s suppose that the phone is most often dropped from about chest height on an average-height person. Second, assume that it is dropped from rest, that is, with an initial vertical velocity of zero. Finally, we assume that the phone bounces very little—the height of its bounce is assumed to be negligible.
Solution
Define upward to be the +y-direction. A typical height is approximately and, as stated, . The average force on the phone is related to the impulse the floor applies on it during the collision:The impulse equals the change in momentum,
so
Next, the change of momentum is
We need to be careful with the velocities here; this is the change of velocity due to the collision with the floor. But the phone also has an initial drop velocity [], so we label our velocities. Let:
- the initial velocity with which the phone was dropped (zero, in this example)
- the velocity the phone had the instant just before it hit the floor
- the final velocity of the phone as a result of hitting the floor
Figure 9.12 shows the velocities at each of these points in the phone’s trajectory.
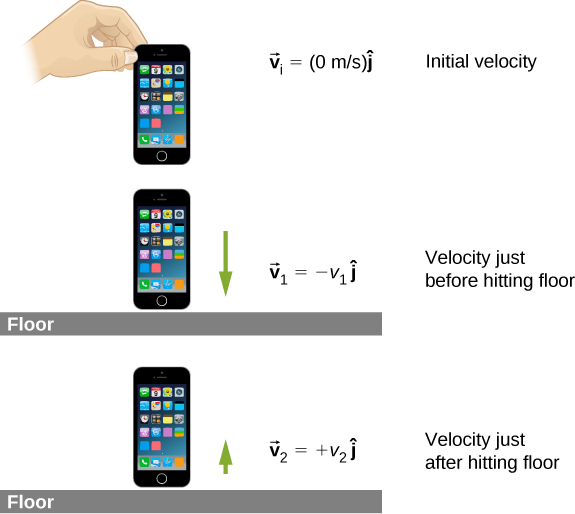
With these definitions, the change of momentum of the phone during the collision with the floor is
Since we assume the phone doesn’t bounce at all when it hits the floor (or at least, the bounce height is negligible), then is zero, so
We can get the speed of the phone just before it hits the floor using either kinematics or conservation of energy. We’ll use conservation of energy here; you should re-do this part of the problem using kinematics and prove that you get the same answer.
First, define the zero of potential energy to be located at the floor. Conservation of energy then gives us:
Defining and using gives
Because is a vector magnitude, it must be positive. Thus, . Inserting this result into the expression for force gives
Finally, we need to estimate the collision time. One common way to estimate a collision time is to calculate how long the object would take to travel its own length. The phone is moving at 5.4 m/s just before it hits the floor, and it is 0.14 m long, giving an estimated collision time of 0.026 s. Inserting the given numbers, we obtain
Significance
The iPhone itself weighs just ; the force the floor applies to it is therefore over 20 times its weight.Check Your Understanding 9.2
What if we had assumed the phone did bounce on impact? Would this have increased the force on the iPhone, decreased it, or made no difference?
Momentum and Force
In Example 9.3, we obtained an important relationship:
In words, the average force applied to an object is equal to the change of the momentum that the force causes, divided by the time interval over which this change of momentum occurs. This relationship is very useful in situations where the collision time is small, but measureable; typical values would be 1/10th of a second, or even one thousandth of a second. Car crashes, punting a football, or collisions of subatomic particles would meet this criterion.
For a continuously changing momentum—due to a continuously changing force—this becomes a powerful conceptual tool. In the limit , Equation 9.2 becomes
This says that the rate of change of the system’s momentum (implying that momentum is a function of time) is exactly equal to the net applied force (also, in general, a function of time). This is, in fact, Newton’s second law, written in terms of momentum rather than acceleration. This is the relationship Newton himself presented in his Principia Mathematica (although he called it “quantity of motion” rather than “momentum”).
If the mass of the system remains constant, Equation 9.3 reduces to the more familiar form of Newton’s second law. We can see this by substituting the definition of momentum:
The assumption of constant mass allowed us to pull m out of the derivative. If the mass is not constant, we cannot use this form of the second law, but instead must start from Equation 9.3. Thus, one advantage to expressing force in terms of changing momentum is that it allows for the mass of the system to change, as well as the velocity; this is a concept we’ll explore when we study the motion of rockets.
Newton’s Second Law of Motion in Terms of Momentum
The net external force on a system is equal to the rate of change of the momentum of that system caused by the force:
Although Equation 9.3 allows for changing mass, as we will see in Rocket Propulsion, the relationship between momentum and force remains useful when the mass of the system is constant, as in the following example.
Example 9.5
Calculating Force: Venus Williams’ Tennis Serve
During the 2007 French Open, Venus Williams hit the fastest recorded serve in a premier women’s match, reaching a speed of 58 m/s (209 km/h). What is the average force exerted on the 0.057-kg tennis ball by Venus Williams’ racquet? Assume that the ball’s speed just after impact is 58 m/s, as shown in Figure 9.13, that the initial horizontal component of the velocity before impact is negligible, and that the ball remained in contact with the racquet for 5.0 ms.
Strategy
This problem involves only one dimension because the ball starts from having no horizontal velocity component before impact. Newton’s second law stated in terms of momentum is then written asAs noted above, when mass is constant, the change in momentum is given by
where we have used scalars because this problem involves only one dimension. In this example, the velocity just after impact and the time interval are given; thus, once is calculated, we can use to find the force.
Solution
To determine the change in momentum, insert the values for the initial and final velocities into the equation above:Now the magnitude of the net external force can be determined by using
where we have retained only two significant figures in the final step.